Sessile drop technique: Difference between revisions
en>Tesi1700 Sorted |
en>Welsh m fix apostrophe per WP:APOSTROPHE |
||
| Line 1: | Line 1: | ||
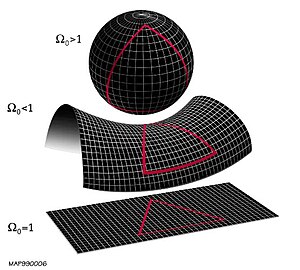
[[Image:End of universe.jpg|thumb|In an Hadamard space, a triangle is [[Hyperbolic triangle|hyperbolic]]; that is, the middle one in the picture. In fact, any complete metric space where a triangle is hyperbolic is an Hadamard space.]] | |||
In [[geometry]], an '''Hadamard space''', named after [[Jacques Hadamard]], is a non-linear generalization of a [[Hilbert space]]. It is defined to be a nonempty<ref>The assumption on "nonempty" has meaning: a fixed point theorem often states the set of fixed point is an Hadamard space. The main content of such an assertion is that the set is nonempty.</ref> complete [[metric space]] where, given any points ''x'', ''y'', there exists a point ''m'' such that for every point ''z'', | |||
:<math>d(z, m)^2 + {d(x, y)^2 \over 4} \le {d(z, x)^2 + d(z, y)^2 \over 2}.</math> | |||
The point ''m'' is then the midpoint of ''x'' and ''y'': <math>d(x, m) = d(y, m) = d(x, y)/2</math>. | |||
In a Hilbert space, the above inequality is equality (with <math>m = (x+y)/2</math>), and in general an Hadamard space is said to be ''flat'' if the above inequality is equality. A flat Hadmard space is isomorphic to a closed convex subset of a Hilbert space. In particular, a [[normed space]] is an Hadamard space if and only if it is a Hilbert space. | |||
The geometry of Hadamard spaces resembles that of Hilbert spaces, making it a natural setting for the study of [[rigidity theorem]]s. In an Hadamard space, any two points can be joined by a unique [[geodesic]] between them; in particular, it is [[contractible space|contractible]]. Quite generally, if ''B'' is a bounded subset of a metric space, then the center of the closed ball of the minimum radius containing it is called the ''[[circumcenter (metric space)|circumcenter]]'' of ''B''.<ref>A Course in Metric Geometry, p. 334.</ref> Every bounded subset of an Hadamard space is contained in the smallest closed ball (which is the same as the closure of its convex hull). If <math>\Gamma</math> is the [[group (mathematics)|group]] of [[isometry|isometries]] of an Hadamard space leaving invariant ''B'', then <math>\Gamma</math> fixes the circumcenter of ''B''. ('''Bruhat–Tits fixed point theorem''') | |||
The basic result for a non-positively curved manifold is the [[Cartan–Hadamard theorem]]. The analog holds for an Hadamard space: a complete, connected metric space which is locally isometric to an Hadamard space has an Hadamard space as its universal cover. Its variant applies for non-positively curved [[orbifold]]s. (cf. Lurie.) | |||
Examples of Hadamard spaces are Hilbert spaces, the [[Poincaré disc]], trees (e.g., [[Bruhat–Tits building]]), [[Cayley graph]]s of [[hyperbolic group]]s or more generally CAT(0) groups, [[(p, q)-space|(''p'', ''q'')-space]] with ''p'', ''q'' ≥ 3 and 2''pq'' ≥ ''p'' + ''q'', and [[Riemannian manifold]]s of nonpositive [[sectional curvature]] (e.g., [[symmetric space]]s). An Hadamard space is precisely a complete [[CAT(k) space|CAT(0) space]]. | |||
== See also == | |||
* [[CAT(k) space]] | |||
== References == | |||
{{reflist}} | |||
*Burago, Dmitri; Yuri Burago, and Sergei Ivanov. ''A Course in Metric Geometry''. American Mathematical Society. (1984) | |||
*[[Jacob Lurie]]: [http://www.math.harvard.edu/~lurie/papers/hadamard.pdf Notes on the Theory of Hadamard Spaces] | |||
[[Category:Hilbert space]] | |||
Revision as of 01:12, 7 December 2013
In geometry, an Hadamard space, named after Jacques Hadamard, is a non-linear generalization of a Hilbert space. It is defined to be a nonempty[1] complete metric space where, given any points x, y, there exists a point m such that for every point z,
The point m is then the midpoint of x and y: .
In a Hilbert space, the above inequality is equality (with ), and in general an Hadamard space is said to be flat if the above inequality is equality. A flat Hadmard space is isomorphic to a closed convex subset of a Hilbert space. In particular, a normed space is an Hadamard space if and only if it is a Hilbert space.
The geometry of Hadamard spaces resembles that of Hilbert spaces, making it a natural setting for the study of rigidity theorems. In an Hadamard space, any two points can be joined by a unique geodesic between them; in particular, it is contractible. Quite generally, if B is a bounded subset of a metric space, then the center of the closed ball of the minimum radius containing it is called the circumcenter of B.[2] Every bounded subset of an Hadamard space is contained in the smallest closed ball (which is the same as the closure of its convex hull). If is the group of isometries of an Hadamard space leaving invariant B, then fixes the circumcenter of B. (Bruhat–Tits fixed point theorem)
The basic result for a non-positively curved manifold is the Cartan–Hadamard theorem. The analog holds for an Hadamard space: a complete, connected metric space which is locally isometric to an Hadamard space has an Hadamard space as its universal cover. Its variant applies for non-positively curved orbifolds. (cf. Lurie.)
Examples of Hadamard spaces are Hilbert spaces, the Poincaré disc, trees (e.g., Bruhat–Tits building), Cayley graphs of hyperbolic groups or more generally CAT(0) groups, (p, q)-space with p, q ≥ 3 and 2pq ≥ p + q, and Riemannian manifolds of nonpositive sectional curvature (e.g., symmetric spaces). An Hadamard space is precisely a complete CAT(0) space.
See also
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- Burago, Dmitri; Yuri Burago, and Sergei Ivanov. A Course in Metric Geometry. American Mathematical Society. (1984)
- Jacob Lurie: Notes on the Theory of Hadamard Spaces



