Cauchy formula for repeated integration: Difference between revisions
en>Wikispaghetti m formula: derivative italic |
en>Addbot m Bot: Migrating 3 interwiki links, now provided by Wikidata on d:q1429231 |
||
| Line 1: | Line 1: | ||
{{Electromagnetism|cTopic=Electrodynamics}} | |||
The '''Maxwell Stress Tensor''' (named after [[James Clerk Maxwell]]) is a '''second rank [[tensor]]''' used in [[classical electromagnetism]] to represent the interaction between electric/magnetic forces and [[momentum|mechanical momentum]]. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the [[Lorentz force law]]. When the situation becomes more complicated, this ordinary procedure can become impossibly difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand. | |||
==Motivation== | |||
[[File:Lorentz force continuum.svg|200px|thumb|Lorentz force (per unit 3-volume) '''f''' on a continuous [[charge distribution]] ([[charge density]] ρ) in motion. The 3-[[current density]] '''J''' corresponds to the motion of the charge element ''dq'' in [[volume element]] ''dV'' and varies throughout the continuum.]] | |||
As outlined below, the electromagnetic force is written in terms of '''E''' and '''B''', using [[vector calculus]] and [[Maxwell's equations]] symmetry in the terms containing '''E''' and '''B''' are sought for, and introducing the Maxwell stress-tensor simplifies the result. | |||
:{| class="wikitable" | |||
|+ Maxwell's equations in SI units in ''vacuum'' <br/> (for reference) | |||
|- | |||
! Name | |||
! Differential form | |||
|- | |||
| Gauss's law (in vacuum) | |||
| <math>\nabla \cdot \mathbf{E} = \frac {\rho} {\epsilon_0}</math> | |||
|- | |||
| Gauss's law for magnetism | |||
| <math>\nabla \cdot \mathbf{B} = 0</math> | |||
|- | |||
| Maxwell–Faraday equation<br />(Faraday's law of induction) | |||
| <math>\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}</math> | |||
|- | |||
| Ampère's circuital law (in vacuum)<br />(with Maxwell's correction) | |||
| <math>\nabla \times \mathbf{B} = \mu_0\mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}} {\partial t}\ </math> | |||
|} | |||
<ol> | |||
<li>Starting with the [[Lorentz force]] law | |||
:<math>\mathbf{F} = q(\mathbf{E} + \mathbf{v}\times\mathbf{B})</math> | |||
the force per unit volume for an unknown charge distribution is | |||
:<math> | |||
\mathbf{f} = \rho\mathbf{E} + \mathbf{J}\times\mathbf{B} | |||
</math></li> | |||
<li>Next, ρ and '''J''' can be replaced by the fields '''E''' and '''B''', using [[Gauss's law]] and [[Ampère's circuital law]]: | |||
:<math> | |||
\mathbf{f} = \epsilon_0 \left(\boldsymbol{\nabla}\cdot \mathbf{E} \right)\mathbf{E} + \frac{1}{\mu_0} \left(\boldsymbol{\nabla}\times \mathbf{B} \right) \times \mathbf{B} - \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \times \mathbf{B}\, | |||
</math></li> | |||
<li>The time derivative can be rewritten to something that can be interpreted physically, namely the [[Poynting vector]]. Using the [[product rule]] and [[Faraday's law of induction]] gives | |||
:<math>\frac{\partial}{\partial t} (\mathbf{E}\times\mathbf{B}) = \frac{\partial\mathbf{E}}{\partial t}\times \mathbf{B} + \mathbf{E} \times \frac{\partial\mathbf{B}}{\partial t} = \frac{\partial\mathbf{E}}{\partial t}\times \mathbf{B} - \mathbf{E} \times (\boldsymbol{\nabla}\times \mathbf{E})\,</math> | |||
and we can now rewrite '''f''' as | |||
:<math>\mathbf{f} = \epsilon_0 \left(\boldsymbol{\nabla}\cdot \mathbf{E} \right)\mathbf{E} + \frac{1}{\mu_0} \left(\boldsymbol{\nabla}\times \mathbf{B} \right) \times \mathbf{B} - \epsilon_0 \frac{\partial}{\partial t}\left( \mathbf{E}\times \mathbf{B}\right) - \epsilon_0 \mathbf{E} \times (\boldsymbol{\nabla}\times \mathbf{E})\,</math>, | |||
then collecting terms with '''E''' and '''B''' gives | |||
:<math>\mathbf{f} = \epsilon_0\left[ (\boldsymbol{\nabla}\cdot \mathbf{E} )\mathbf{E} - \mathbf{E} \times (\boldsymbol{\nabla}\times \mathbf{E}) \right] + \frac{1}{\mu_0} \left[ - \mathbf{B}\times\left(\boldsymbol{\nabla}\times \mathbf{B} \right) \right] | |||
- \epsilon_0\frac{\partial}{\partial t}\left( \mathbf{E}\times \mathbf{B}\right)\,</math>.</li> | |||
<li>A term seems to be "missing" from the symmetry in '''E''' and '''B''', which can be achieved by inserting (∇ • '''B''')'''B''' because of [[Gauss' law for magnetism]]: | |||
:<math>\mathbf{f} = \epsilon_0\left[ (\boldsymbol{\nabla}\cdot \mathbf{E} )\mathbf{E} - \mathbf{E} \times (\boldsymbol{\nabla}\times \mathbf{E}) \right] + \frac{1}{\mu_0} \left[(\boldsymbol{\nabla}\cdot \mathbf{B} )\mathbf{B} - \mathbf{B}\times\left(\boldsymbol{\nabla}\times \mathbf{B} \right) \right] | |||
- \epsilon_0\frac{\partial}{\partial t}\left( \mathbf{E}\times \mathbf{B}\right)\,</math>. | |||
Eliminating the curls (which are fairly complicated to calculate), using the [[vector calculus identity]] | |||
:<math>\tfrac{1}{2} \boldsymbol{\nabla} (\mathbf{A}\cdot\mathbf{A}) = \mathbf{A} \times (\boldsymbol{\nabla} \times \mathbf{A}) + (\mathbf{A} \cdot \boldsymbol{\nabla}) \mathbf{A} </math>, | |||
leads to: | |||
:<math>\mathbf{f} = \epsilon_0\left[ (\boldsymbol{\nabla}\cdot \mathbf{E} )\mathbf{E} + (\mathbf{E}\cdot\boldsymbol{\nabla}) \mathbf{E} \right] + \frac{1}{\mu_0} \left[(\boldsymbol{\nabla}\cdot \mathbf{B} )\mathbf{B} + (\mathbf{B}\cdot\boldsymbol{\nabla}) \mathbf{B} \right] - \frac{1}{2} \boldsymbol{\nabla}\left(\epsilon_0 E^2 + \frac{1}{\mu_0} B^2 \right) | |||
- \epsilon_0\frac{\partial}{\partial t}\left( \mathbf{E}\times \mathbf{B}\right)\,</math>.</li> | |||
<li>This expression contains every aspect of electromagnetism and momentum and is relatively easy to compute. It can be written more compactly by introducing the '''Maxwell stress tensor''', | |||
:<math>\sigma_{i j} \equiv \epsilon_0 \left(E_i E_j - \frac{1}{2} \delta_{ij} E^2\right) + \frac{1}{\mu_0} \left(B_i B_j - \frac{1}{2} \delta_{ij} B^2\right)\,</math>, | |||
and notice that all but the last term of the above can be written as the [[divergence]] of this: | |||
:<math>\mathbf{f} + \epsilon_0 \mu_0 \frac{\partial \mathbf{S}}{\partial t}\, = \nabla \cdot \mathbf{\sigma}</math>, | |||
As in the [[Poynting's theorem]], the second term in the left side of above equation can be interpreted as time derivative of EM field's momentum density and this way, the above equation will be the law of conservation of momentum in classical electrodynamics. | |||
where we have finally introduced the [[Poynting vector]], | |||
:<math>\mathbf{S} = \frac{1}{\mu_0}\mathbf{E}\times\mathbf{B}</math>.</li> | |||
</ol> | |||
in the above relation for conservation of momentum, <math>\nabla \cdot \mathbf{\sigma}</math> is the '''momentum flux density''' and plays a role similar to <math>\mathbf{S}</math> in [[Poynting's theorem]]. | |||
==Equation== | |||
In [[physics]], the '''Maxwell stress tensor''' is the [[stress tensor]] of an [[electromagnetic field]]. As derived above in [[SI unit]]s, it is given by: | |||
:<math>\sigma_{i j} = \epsilon_0 E_i E_j + \frac{1} | |||
{{\mu _0 }}B_i B_j - \frac{1}{2}\bigl( {\epsilon_0 E^2 + \tfrac{1} | |||
{{\mu _0 }}B^2 } \bigr)\delta _{ij} </math>, | |||
where ε<sub>0</sub> is the [[electric constant]] and μ<sub>0</sub> is the [[magnetic constant]], '''E''' is the [[electric field]], '''B''' is the [[magnetic field]] and δ<sub>''ij''</sub> is [[Kronecker's delta]]. In Gaussian [[cgs unit]], it is given by: | |||
:<math>\sigma_{i j}=\frac{1}{4\pi}\left(E_{i}E_{j}+H_{i}H_{j}- | |||
\frac{1}{2}(E^2+H^2)\delta_{ij}\right)</math>, | |||
where '''H''' is the [[magnetizing field]]. | |||
An alternative way of expressing this tensor is: | |||
:<math> | |||
\overset{\leftrightarrow }{ \mathbf{\sigma} } = \frac{1}{4\pi} \left[ \mathbf{E}\otimes\mathbf{E} + \mathbf{H}\otimes\mathbf{H} - \frac{E^2+H^2 }{2} (\mathbf{\hat x}\otimes\mathbf{\hat x} + \mathbf{\hat y}\otimes\mathbf{\hat y} + \mathbf{\hat z}\otimes\mathbf{\hat z}) \right] | |||
</math>, | |||
where ⊗ is the [[dyadic product]]. | |||
The element ''ij'' of the Maxwell stress tensor has units of momentum per unit of area times time and gives the flux of momentum parallel to the ''i''th axis crossing a surface normal to the ''j''th axis (in the negative direction) per unit of time. | |||
These units can also be seen as units of force per unit of area (negative pressure), and the ''ij'' element of the tensor can also be interpreted as the force parallel to the ''i''th axis suffered by a surface normal to the jth axis per unit of area. Indeed the diagonal elements give the [[tension (physics)|tension]] (pulling) acting on a differential area element normal to the corresponding axis. Unlike forces due to the pressure of an ideal gas, an area element in the electromagnetic field also feels a force in a direction that is not normal to the element. This shear is given by the off-diagonal elements of the stress tensor. | |||
==Magnetism only== | |||
If the field is only magnetic (which is largely true in motors, for instance), some of the terms drop out, and the equation in SI units becomes: | |||
:<math>\sigma_{i j} = \frac{1}{\mu_0} B_i B_j - \frac{1}{2 \mu_0} B^2 \delta_{i j} \,.</math> | |||
For cylindrical objects, such as the rotor of a motor, this is further simplified to: | |||
:<math>\sigma_{r t} = \frac{1}{\mu_0} B_r B_t - \frac{1}{2 \mu_0} B^2 \delta_{r t} \,.</math> | |||
where ''r'' is the shear in the radial (outward from the cylinder) direction, and ''t'' is the shear in the tangential (around the cylinder) direction. It is the tangential force which spins the motor. ''B''<sub>''r''</sub> is the flux density in the radial direction, and ''B''<sub>''t''</sub> is the flux density in the tangential direction. | |||
== See also == | |||
*[[Ricci calculus]] | |||
*[[Energy density#Energy density of electric and magnetic fields|Energy density of electric and magnetic fields]] | |||
*[[Poynting vector]] | |||
*[[Electromagnetic stress-energy tensor]] | |||
*[[Magnetic pressure]] | |||
*[[Magnetic tension force]] | |||
==References== | |||
* David J. Griffiths,"Introduction to Electrodynamics" pp. 351–352, Benjamin Cummings Inc., 2008 | |||
* John David Jackson,"Classical Electrodynamics, 3rd Ed.", John Wiley & Sons, Inc., 1999. | |||
* Richard Becker,"Electromagnetic Fields and Interactions",Dover Publications Inc., 1964. | |||
[[Category:Tensors]] | |||
[[Category:Electromagnetism]] | |||
Latest revision as of 21:41, 6 March 2013
Earlier than you determine whether or not stainless steel cookware is value shopping for, lets first talk about what stainless steel cookware is. Chrome steel is made from an alloy, or a mix of metals. Mostly, fundamental iron with chromium, nickel or some other minor metals. The chromium supplies rust protection and provides your cookware sturdiness. The nickel provides rust safety as effectively, and provides a refined look. Most effectively made chrome steel cookware has copper or aluminum added to the underside of the pan or pot. This is finished to increases the ability of the pot or pan to conduct heat.
One of the best stainless-steel cookware is the principle category, however nonetheless it is divided into several subcategories based mostly on the quality and the price range. It may be confusing to decide on the very best stainless-steel cookware out of the categories that may meet your requirements. That is where we took a step forward to explain you all the knowledge that will likely be helpful so that you can understand how to decide on the best chrome steel cookware. The best stainless-steel cookware set is manufactured from low-cost to expensive and quality constructed pots and pans.
You will find magnetic stainless steel within the layer on the outside of some high quality pieces of stainless-steel. That is to make it compatible with induction stovetops, which involve using a rapidly charging electromagnetic subject to warmth cookware. High-high quality stainless steel, like All-Clad , uses three layers of steel—the austenite layer of metal on the within, ferrite steel on the outside, and a layer of aluminum sandwiched between the two for optimum heat conductivity (metal alone doesn't conduct warmth evenly). Lesser-high quality stainless-steel is usually only one layer of austenitic chrome steel.
Aesthetically talking, chrome steel is a wise alternative when you favor to show or hang pots or pans. The clean, crisp look of all chrome steel kitchenware can remodel a mishmash of cookware into a complicated décor statement. Chrome steel kettles, such because the Cuisinart Tea Kettle will combine individual kitchenware right into a cohesive and nice entity. Take into account buying stainless-steel utensils as well. Already acquired a gorgeous stainless steel cookware assortment? The Cuisinart Chef’s Collection stainless pot rack could be the crowning glory for a kitchen, liberating up space and making these pots and pans readily accessible. Get the stainless-steel cookware of your culinary goals at Macy’s!
Arduous-anodized aluminum cookware is among the most popular forms of material, despite the fact that many people do not fairly perceive the development. Hard-anodized aluminum is plain aluminum that has been processed in a series of chemical baths charged with an electrical present. The result's a fabric that has the same superior warmth conductivity as aluminum however is non-reactive with acidic meals, similar to tomatoes, and twice as hard as chrome steel. Two drawbacks to laborious-anodized cookware are that it's not dishwasher-secure and, because it isn't magnetic, it will not work with induction range tops.
The enamel over metal method creates a piece that has the heat distribution of carbon steel and a non-reactive, low-stick surface. In the event you loved this information and you desire to acquire details about best stainless steel cookware i implore you to pay a visit to our page. Such pots are a lot lighter than most different pots of comparable dimension, are cheaper to make than chrome steel pots, and would not have the rust and reactivity problems with forged iron or carbon steel. quotation needed Enamel over metal is right for large stockpots and for different giant pans used mostly for water-primarily based cooking. Because of its mild weight and simple cleanup, enamel over metal can also be standard for cookware used while tenting. Clad aluminium or copper edit
Unique specialty cookware items served a la carte to compliment any cookware set are constructed of a sturdy Stainless Steel with a brushed exterior finish. Designed with an impression bonded, aluminum disk encapsulated base which distributes warmth quickly and evenly to permit exact temperature management. Handles are riveted for durability and efficiency. The New Specialty Cookware is compatible for all vary sorts together with induction. Along with the multi use function, another unique characteristic is bottom to top interior quantity markings in each quarts and metric measurement; and each bit comes with a tempered glass lid, oven safe to 350°F.
Whether or not you are a cooking enthusiasts, knowledgeable chef or simply cooking for your family you know the importance of getting a totally stocked kitchen. Not solely do you want the fitting elements, but you also need the right instruments to get the job performed. In any sort of fundamental cooking coaching lesson, you will be taught that chrome steel is your new finest pal when it comes to kitchen cookware. What additionally, you will study is that quality cooking tools does not normally come at a reduced price. Because of this, you will need to take good care of your cookware! Listed here are some fundamentals for stainless steel care.
To combat the uneven heating downside, most stainless steel pans are laminations of aluminum or copper on the underside to spread the warmth around, and stainless-steel contained in the pan to provide a cooking floor that's impervious to whatever you might put inside. In my experience, this chrome steel floor continues to be too sticky to fry on, and when you ever burn it you get a permanent hassle spot. But, sometimes a stainless-steel cooking surface turns out to be useful when you can't use aluminum (see below) so I keep some round. Choose one thing with a fairly thick aluminum layer on the underside.
Well, until you’re a metals professional and go examine the factory where the steel is made to see whether or not their manufacturing course of creates a pure austenite without corrosive supplies shaped, you’re not going to know for sure whether or not the craftsmanship of your stainless is of the very best quality. I think your greatest wager is to simply buy high-quality chrome steel from the start, from a brand with a reputation for good quality. But, I believe I have found out one way that you would be able to decide if the stainless cookware you already have is probably reactive.
The Maxwell Stress Tensor (named after James Clerk Maxwell) is a second rank tensor used in classical electromagnetism to represent the interaction between electric/magnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impossibly difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.
Motivation
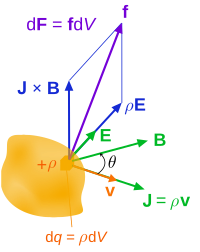
As outlined below, the electromagnetic force is written in terms of E and B, using vector calculus and Maxwell's equations symmetry in the terms containing E and B are sought for, and introducing the Maxwell stress-tensor simplifies the result.
- Starting with the Lorentz force law the force per unit volume for an unknown charge distribution is
- Next, ρ and J can be replaced by the fields E and B, using Gauss's law and Ampère's circuital law:
- The time derivative can be rewritten to something that can be interpreted physically, namely the Poynting vector. Using the product rule and Faraday's law of induction gives and we can now rewrite f as then collecting terms with E and B gives
- A term seems to be "missing" from the symmetry in E and B, which can be achieved by inserting (∇ • B)B because of Gauss' law for magnetism: Eliminating the curls (which are fairly complicated to calculate), using the vector calculus identity leads to:
- This expression contains every aspect of electromagnetism and momentum and is relatively easy to compute. It can be written more compactly by introducing the Maxwell stress tensor, and notice that all but the last term of the above can be written as the divergence of this: As in the Poynting's theorem, the second term in the left side of above equation can be interpreted as time derivative of EM field's momentum density and this way, the above equation will be the law of conservation of momentum in classical electrodynamics. where we have finally introduced the Poynting vector,
in the above relation for conservation of momentum, is the momentum flux density and plays a role similar to in Poynting's theorem.
Equation
In physics, the Maxwell stress tensor is the stress tensor of an electromagnetic field. As derived above in SI units, it is given by:
where ε0 is the electric constant and μ0 is the magnetic constant, E is the electric field, B is the magnetic field and δij is Kronecker's delta. In Gaussian cgs unit, it is given by:
where H is the magnetizing field.
An alternative way of expressing this tensor is:
where ⊗ is the dyadic product.
The element ij of the Maxwell stress tensor has units of momentum per unit of area times time and gives the flux of momentum parallel to the ith axis crossing a surface normal to the jth axis (in the negative direction) per unit of time.
These units can also be seen as units of force per unit of area (negative pressure), and the ij element of the tensor can also be interpreted as the force parallel to the ith axis suffered by a surface normal to the jth axis per unit of area. Indeed the diagonal elements give the tension (pulling) acting on a differential area element normal to the corresponding axis. Unlike forces due to the pressure of an ideal gas, an area element in the electromagnetic field also feels a force in a direction that is not normal to the element. This shear is given by the off-diagonal elements of the stress tensor.
Magnetism only
If the field is only magnetic (which is largely true in motors, for instance), some of the terms drop out, and the equation in SI units becomes:
For cylindrical objects, such as the rotor of a motor, this is further simplified to:
where r is the shear in the radial (outward from the cylinder) direction, and t is the shear in the tangential (around the cylinder) direction. It is the tangential force which spins the motor. Br is the flux density in the radial direction, and Bt is the flux density in the tangential direction.
See also
- Ricci calculus
- Energy density of electric and magnetic fields
- Poynting vector
- Electromagnetic stress-energy tensor
- Magnetic pressure
- Magnetic tension force
References
- David J. Griffiths,"Introduction to Electrodynamics" pp. 351–352, Benjamin Cummings Inc., 2008
- John David Jackson,"Classical Electrodynamics, 3rd Ed.", John Wiley & Sons, Inc., 1999.
- Richard Becker,"Electromagnetic Fields and Interactions",Dover Publications Inc., 1964.