Gauss's law for gravity: Difference between revisions
en>Maschen m →Derivation from Lagrangian: make link apperances cleaner (very minor change) |
en>Milad pourrahmani |
||
| Line 1: | Line 1: | ||
'''Free spectral range''' ('''FSR''') is the spacing in optical [[frequency]] or [[wavelength]] between two successive reflected or transmitted optical intensity maxima or minima of an [[interferometer]] or [[diffractive optical element]]. | |||
The FSR is not always represented by <math>\Delta\nu</math> or <math>\Delta\lambda</math>, but instead is some times only represented by the letters FSR. The reason is because these difference terms often refer to the bandwidth or linewidth of an emitted source respectively. | |||
== In General == | |||
The free spectral range(FSR) of a cavity is given by: | |||
:<math>\Delta\nu=\frac{c}{2n_gl}</math> | |||
Where <math>l</math> is the length of the cavity, <math>n_g</math> is the [[group index]] of the media within the cavity and <math>c</math> is the speed of light. | |||
In wavelength, the FSR is given by: | |||
:<math>\Delta\lambda=\frac{\lambda^2}{2n_gl}</math> | |||
Where <math>\lambda</math> is the wavelength of light in the cavity. | |||
== Diffraction gratings == | |||
The free spectral range of a [[diffraction grating]] is the largest wavelength range for a given order that does not overlap the same range in an adjacent order. If the (''m''+1)<sup>th</sup> order of <math>\lambda</math> and (''m'')<sup>th</sup> order of <math>(\lambda + \Delta \lambda)</math> lie at the same angle, then | |||
:<math>\Delta \lambda={\lambda \over m}</math> | |||
== Fabry–Pérot interferometer == | |||
In a [[Fabry–Pérot interferometer]] or etalon, the wavelength separation between adjacent transmission peaks is called the free spectral range of the etalon, and is given by: | |||
:<math>\Delta\lambda = \frac{ \lambda_0^2}{2nl \cos\theta + \lambda_0 } \approx \frac{ \lambda_0^2}{2nl \cos\theta } </math> | |||
where λ<sub>0</sub> is the central wavelength of the nearest transmission peak, ''n'' is the [[index of refraction]] of the cavity medium, <math>\theta</math> is the angle of incidence, and ''l'' is the thickness of the cavity. More often FSR is quoted in frequency, rather than wavelength units: | |||
:<math>\Delta f \approx \frac{ c}{2nl \cos\theta } </math> | |||
[[Image:Etalon-2.png|frame|right|The transmission of an etalon as a function of wavelength. A high-finesse etalon (red line) shows sharper peaks and lower transmission minima than a low-finesse etalon (blue). The free spectral range is Δλ (shown above the graph).]] | |||
The FSR is related to the full-width half-maximum, δλ, of any one transmission band by a quantity known as the ''finesse'': | |||
:<math> \mathcal{F} = \frac{\Delta\lambda}{\delta\lambda}=\frac{\pi}{2 \arcsin(1/\sqrt F)},</math> | |||
where <math> F = \frac{4R}{{(1-R)^2}}</math> is the ''coefficient of finesse'', and R is the reflectivity of the mirrors. | |||
This is commonly approximated (for ''R'' > 0.5) by | |||
:<math> \mathcal{F} \approx \frac{\pi \sqrt{F}}{2}=\frac{\pi R^{1/2} }{(1-R)}. </math> | |||
[[Category:Physical optics]] | |||
{{optics-stub}} | |||
Revision as of 18:21, 5 August 2013
Free spectral range (FSR) is the spacing in optical frequency or wavelength between two successive reflected or transmitted optical intensity maxima or minima of an interferometer or diffractive optical element.
The FSR is not always represented by or , but instead is some times only represented by the letters FSR. The reason is because these difference terms often refer to the bandwidth or linewidth of an emitted source respectively.
In General
The free spectral range(FSR) of a cavity is given by:
Where is the length of the cavity, is the group index of the media within the cavity and is the speed of light.
In wavelength, the FSR is given by:
Where is the wavelength of light in the cavity.
Diffraction gratings
The free spectral range of a diffraction grating is the largest wavelength range for a given order that does not overlap the same range in an adjacent order. If the (m+1)th order of and (m)th order of lie at the same angle, then
Fabry–Pérot interferometer
In a Fabry–Pérot interferometer or etalon, the wavelength separation between adjacent transmission peaks is called the free spectral range of the etalon, and is given by:
where λ0 is the central wavelength of the nearest transmission peak, n is the index of refraction of the cavity medium, is the angle of incidence, and l is the thickness of the cavity. More often FSR is quoted in frequency, rather than wavelength units:
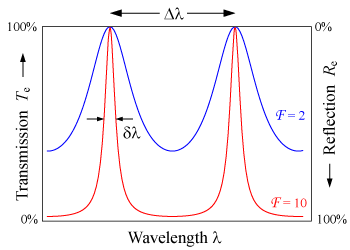
The FSR is related to the full-width half-maximum, δλ, of any one transmission band by a quantity known as the finesse:
where is the coefficient of finesse, and R is the reflectivity of the mirrors.
This is commonly approximated (for R > 0.5) by