Reduced viscosity: Difference between revisions
en>Malcolma added Category:Viscosity; removed {{uncategorized}} using HotCat |
en>Omkar Paropkari m Just changed a common word (viscosity) into a link. That gives the article a "parent", right? :) |
||
| Line 1: | Line 1: | ||
{| class=wikitable width=280 align=right style="margin-left:1em" | |||
!<math>{\tilde{A}}_2</math> | |||
!<math>{\tilde{A}}_3</math> | |||
|- | |||
![[Triangular tiling]] | |||
![[Tetrahedral-octahedral honeycomb]] | |||
|- | |||
|[[File:Uniform_tiling_333-t1.png|120px]]<BR>With red and yellow equilateral triangles | |||
|[[File:Tetrahedral-octahedral honeycomb2.png|160px]]<BR>With cyan and yellow [[tetrahedron|tetrahedra]], and red rectified tetrahedra ([[octahedron]]) | |||
|- | |||
!{{CDD|node_1|split1|branch}} | |||
!{{CDD|node_1|split1|nodes|split2|node}} | |||
|} | |||
In [[geometry]], the '''simplectic honeycomb''' (or '''n-simplex honeycomb''') is a dimensional infinite series of [[Honeycomb (geometry)|honeycomb]]s, based on the <math>{\tilde{A}}_n</math> affine [[Coxeter group]] symmetry. It is given a [[Schläfli symbol]] {3<sup>[n+1]</sup>}, and is represented by a [[Coxeter-Dynkin diagram]] as a cyclic graph of ''n+1'' nodes with one node ringed. It is composed of n-[[simplex]] facets, along with all [[Rectification (geometry)|rectified]] n-simplices. The [[vertex figure]] of an ''n-simplex honeycomb'' is an [[Expansion (geometry)|expanded]] n-[[simplex]]. | |||
In 2 dimensions, the honeycomb represents the [[triangular tiling]], with Coxeter graph {{CDD|node_1|split1|branch}} filling the plane with alternately colored triangles. In 3 dimensions it represents the [[tetrahedral-octahedral honeycomb]], with Coxeter graph {{CDD|node_1|split1|nodes|split2|node}} filling space with alternately tetrahedral and octahedral cells. In 4 dimensions it is called the [[5-cell honeycomb]], with Coxeter graph {{CDD|node_1|split1|nodes|3ab|branch}}, with [[5-cell]] and [[rectified 5-cell]] facets. In 5 dimensions it is called the [[5-simplex honeycomb]], with Coxeter graph {{CDD|node_1|split1|nodes|3ab|nodes|split2|node}}, filling space by [[5-simplex]], [[rectified 5-simplex]], and [[birectified 5-simplex]] facets. In 6 dimensions it is called the [[6-simplex honeycomb]], with Coxeter graph {{CDD|node_1|split1|nodes|3ab|nodes|3ab|branch}}, filling space by [[6-simplex]], [[rectified 6-simplex]], and [[birectified 6-simplex]] facets. | |||
== By dimension == | |||
{| class="wikitable" | |||
!height=30|n | |||
!<math>{\tilde{A}}_{2+}</math> | |||
!Tessellation | |||
!Vertex figure | |||
!Facets per vertex figure | |||
!Vertices per vertex figure | |||
!Edge figure | |||
|- align=center | |||
|1 | |||
|<math>{\tilde{A}}_1</math> | |||
|[[File:Regular_apeirogon.png|80px]]<BR>[[Apeirogon]]<BR>{{CDD|node_1|infin|node}} | |||
|{{CDD|node_1}} | |||
|1 | |||
|2 | |||
| - | |||
|- align=center | |||
|2 | |||
|<math>{\tilde{A}}_2</math> | |||
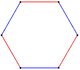
|[[Image:Uniform tiling 333-t1.png|80px]]<BR>[[Triangular tiling]]<BR>2-simplex honeycomb<BR>{{CDD|node_1|split1|branch}} | |||
|[[Image:Truncated triangle.png|80px]]<BR>[[Hexagon]]<BR>(Truncated triangle)<BR>{{CDD|node_1|3|node_1}} | |||
|3 [[triangle]]s<BR>3 [[hexagon|rectified triangles]] | |||
|6 | |||
|[[Line segment]]<BR>{{CDD|node_1}} | |||
|- align=center | |||
|3 | |||
|<math>{\tilde{A}}_3</math> | |||
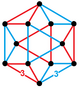
|[[File:Tetrahedral-octahedral honeycomb2.png|80px]]<BR>[[Tetrahedral-octahedral honeycomb]]<BR>3-simplex honeycomb<BR>{{CDD|node_1|split1|nodes|split2|node}} | |||
|[[File:Uniform_t0_3333_honeycomb_verf2.png|80px]]<BR>[[Cuboctahedron]]<BR>(Cantellated tetrahedron)<BR>{{CDD|node_1|3|node|3|node_1}} | |||
|4+4 [[tetrahedron]]<BR>6 [[octahedron|rectified tetrahedra]] | |||
|12 | |||
|[[File:Cuboctahedron vertfig.png|60px]]<BR>[[Rectangle]]<BR>{{CDD|node_1|2|node_1}} | |||
|- align=center | |||
|4 | |||
|<math>{\tilde{A}}_4</math> | |||
|[[4-simplex honeycomb]]<BR>{{CDD|node_1|split1|nodes|3ab|branch}} | |||
|[[File:4-simplex_honeycomb_verf.png|80px]]<BR>[[Runcinated 5-cell]]<BR>{{CDD|node_1|3|node|3|node|3|node_1}} | |||
|5+5 [[5-cell]]s<BR>10+10 [[rectified 5-cell]]s | |||
|20 | |||
|[[File:Runcinated_5-cell_verf.png|60px]]<BR>Triangular antiprism<BR>{{CDD|node_h|3|node_h|2|node_h}} | |||
|- align=center | |||
|5 | |||
|<math>{\tilde{A}}_5</math> | |||
|[[5-simplex honeycomb]]<BR>{{CDD|node_1|split1|nodes|3ab|nodes|split2|node}} | |||
|[[File:5-simplex_t04_A4.svg|80px]]<BR>[[Stericated 5-simplex]]<BR>{{CDD|node_1|3|node|3|node|3|node|3|node_1}} | |||
|6+6 [[5-simplex]]<BR>15+15 [[rectified 5-simplex]]<BR>20 [[birectified 5-simplex]] | |||
|30 | |||
|[[File:Stericated_hexateron_verf.png|60px]]<BR>Tetrahedral antiprism<BR>{{CDD|node|3|node|4|node_h|2|node_h}} | |||
|- align=center | |||
|6 | |||
|<math>{\tilde{A}}_6</math> | |||
|[[6-simplex honeycomb]]<BR>{{CDD|node_1|split1|nodes|3ab|nodes|3ab|branch}} | |||
|[[File:6-simplex_t05.svg|80px]]<BR>[[Pentellated 6-simplex]]<BR>{{CDD|node_1|3|node|3|node|3|node|3|node|3|node_1}} | |||
|7+7 [[6-simplex]]<BR>21+21 [[rectified 6-simplex]]<BR>35+35 [[birectified 6-simplex]] | |||
|42 | |||
|4-simplex antiprism | |||
|- align=center | |||
|7 | |||
|<math>{\tilde{A}}_7</math> | |||
|[[7-simplex honeycomb]]<BR>{{CDD|node_1|split1|nodes|3ab|nodes|3ab|nodes|split2|node}} | |||
|[[File:7-simplex_t06_A6.svg|80px]]<BR>[[Hexicated 7-simplex]]<BR>{{CDD|node_1|3|node|3|node|3|node|3|node|3|node|3|node_1}} | |||
|8+8 [[7-simplex]]<BR>28+28 [[rectified 7-simplex]]<BR>56+56 [[birectified 7-simplex]]<BR>70 [[trirectified 7-simplex]] | |||
|56 | |||
|5-simplex antiprism | |||
|- align=center | |||
|8 | |||
|<math>{\tilde{A}}_8</math> | |||
|[[8-simplex honeycomb]]<BR>{{CDD|node_1|split1|nodes|3ab|nodes|3ab|nodes|3ab|branch}} | |||
|[[File:8-simplex_t07.svg|80px]]<BR>[[Heptellated 8-simplex]]<BR>{{CDD|node_1|3|node|3|node|3|node|3|node|3|node|3|node|3|node_1}} | |||
|9+9 [[8-simplex]]<BR>36+36 [[rectified 8-simplex]]<BR>84+84 [[birectified 8-simplex]]<BR>126+126 [[trirectified 8-simplex]] | |||
|72 | |||
|6-simplex antiprism | |||
|- align=center | |||
|9 | |||
|<math>{\tilde{A}}_9</math> | |||
|[[9-simplex honeycomb]]<BR>{{CDD|node_1|split1|nodes|3ab|nodes|3ab|nodes|3ab|nodes|split2|node}} | |||
|[[File:9-simplex_t08.svg|80px]]<BR>[[Octellated 9-simplex]]<BR>{{CDD|node_1|3|node|3|node|3|node|3|node|3|node|3|node|3|node|3|node_1}} | |||
|10+10 [[9-simplex]]<BR>45+45 [[rectified 9-simplex]]<BR>120+120 [[birectified 9-simplex]]<br>210+210 [[trirectified 9-simplex]]<br>252 [[quadrirectified 9-simplex]] | |||
|90 | |||
|7-simplex antiprism | |||
|- align=center | |||
|10 | |||
|<math>{\tilde{A}}_{10}</math> | |||
|[[10-simplex honeycomb]]<BR>{{CDD|node_1|split1|nodes|3ab|nodes|3ab|nodes|3ab|nodes|3ab|branch}} | |||
|[[File:10-simplex_t09.svg|80px]]<BR>[[Ennecated 10-simplex]]<BR>{{CDD|node_1|3|node|3|node|3|node|3|node|3|node|3|node|3|node|3|node|3|node_1}} | |||
|11+11 [[10-simplex]]<BR>55+55 [[rectified 10-simplex]]<BR>165+165 [[birectified 10-simplex]]<BR>330+330 [[trirectified 10-simplex]]<BR>462+462 [[quadrirectified 10-simplex]] | |||
|110 | |||
|8-simplex antiprism | |||
|- align=center | |||
|11 | |||
|<math>{\tilde{A}}_{11}</math> | |||
|11-simplex honeycomb | |||
|... | |||
|... | |||
|... | |||
|... | |||
|} | |||
== Projection by folding == | |||
The (2n-1)-simplex honeycombs and 2n-simplex honeycombs can be projected into the n-dimensional [[hypercubic honeycomb]] by a [[Coxeter–Dynkin diagram#Geometric folding|geometric folding]] operation that maps two pairs of mirrors into each other, sharing the same [[vertex arrangement]]: | |||
{|class=wikitable | |||
|- | |||
!<math>{\tilde{A}}_2</math> | |||
|{{CDD|node_1|split1|branch}} | |||
!<math>{\tilde{A}}_4</math> | |||
|{{CDD|node_1|split1|nodes|3ab|branch}} | |||
!<math>{\tilde{A}}_6</math> | |||
|{{CDD|node_1|split1|nodes|3ab|nodes|3ab|branch}} | |||
!<math>{\tilde{A}}_8</math> | |||
|{{CDD|node_1|split1|nodes|3ab|nodes|3ab|nodes|3ab|branch}} | |||
!<math>{\tilde{A}}_{10}</math> | |||
|{{CDD|node_1|split1|nodes|3ab|nodes|3ab|nodes|3ab|nodes|3ab|branch}} | |||
|... | |||
|- | |||
!<math>{\tilde{A}}_3</math> | |||
|{{CDD|nodes_10r|splitcross|nodes}} | |||
!<math>{\tilde{A}}_3</math> | |||
|{{CDD|node_1|split1|nodes|split2|node}} | |||
!<math>{\tilde{A}}_5</math> | |||
|{{CDD|node_1|split1|nodes|3ab|nodes|split2|node}} | |||
!<math>{\tilde{A}}_7</math> | |||
|{{CDD|node_1|split1|nodes|3ab|nodes|3ab|nodes|split2|node}} | |||
!<math>{\tilde{A}}_9</math> | |||
|{{CDD|node_1|split1|nodes|3ab|nodes|3ab|nodes|3ab|nodes|split2|node}} | |||
|... | |||
|- | |||
!<math>{\tilde{C}}_1</math> | |||
|{{CDD|node_1|infin|node}} | |||
!<math>{\tilde{C}}_2</math> | |||
|{{CDD|node_1|4|node|4|node}} | |||
!<math>{\tilde{C}}_3</math> | |||
|{{CDD|node_1|4|node|3|node|4|node}} | |||
!<math>{\tilde{C}}_4</math> | |||
|{{CDD|node_1|4|node|3|node|3|node|4|node}} | |||
!<math>{\tilde{C}}_5</math> | |||
|{{CDD|node_1|4|node|3|node|3|node|3|node|4|node}} | |||
|... | |||
|} | |||
== Kissing number == | |||
These honeycombs, seen as tangent n-spheres located at the center of each honeycomb vertex have a fixed number of contacting spheres and correspond to the number of vertices in the [[vertex figure]]. For 2 and 3 dimensions, this represents the highest [[kissing number]] for 2 and 3 dimensions, but fall short on higher dimensions. In 2-dimensions, the triangular tiling defines a circle packing of 6 tangent spheres arranged in a regular hexagon, and for 3 dimensions there are 12 tangent spheres arranged in an [[cuboctahedron|cuboctahedral]] configuration. For 4 to 8 dimensions, the kissing numbers are [[Expanded 4-simplex|20]], [[Expanded 5-simplex|30]], [[Expanded 5-simplex|42]], [[Expanded 6-simplex|56]], and [[Expanded 7-simplex|72]] spheres, while the greatest solutions are 24, 40, 72, 126, and 240 spheres respectively. | |||
== See also== | |||
* [[Hypercubic honeycomb]] | |||
* [[Alternated hypercubic honeycomb]] | |||
* [[Quarter hypercubic honeycomb]] | |||
* [[Truncated simplectic honeycomb]] | |||
* [[Omnitruncated simplectic honeycomb]] | |||
== References == | |||
* [[George Olshevsky]], ''Uniform Panoploid Tetracombs'', Manuscript (2006) ''(Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)'' | |||
* [[Branko Grünbaum]], Uniform tilings of 3-space. [[Geombinatorics]] 4(1994), 49 - 56. | |||
* [[Norman Johnson (mathematician)|Norman Johnson]] ''Uniform Polytopes'', Manuscript (1991) | |||
* [[Coxeter|Coxeter, H.S.M.]] ''[[Regular Polytopes (book)|Regular Polytopes]]'', (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 | |||
* '''Kaleidoscopes: Selected Writings of H.S.M. Coxeter''', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html] | |||
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings) | |||
** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', [Math. Zeit. 200 (1988) 3-45] | |||
{{Honeycombs}} | |||
[[Category:Honeycombs (geometry)]] | |||
[[Category:Polytopes]] | |||
Latest revision as of 12:44, 23 September 2013
| Triangular tiling | Tetrahedral-octahedral honeycomb |
|---|---|
 With red and yellow equilateral triangles |
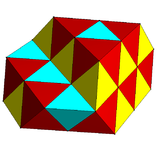 With cyan and yellow tetrahedra, and red rectified tetrahedra (octahedron) |
| Template:CDD | Template:CDD |
In geometry, the simplectic honeycomb (or n-simplex honeycomb) is a dimensional infinite series of honeycombs, based on the affine Coxeter group symmetry. It is given a Schläfli symbol {3[n+1]}, and is represented by a Coxeter-Dynkin diagram as a cyclic graph of n+1 nodes with one node ringed. It is composed of n-simplex facets, along with all rectified n-simplices. The vertex figure of an n-simplex honeycomb is an expanded n-simplex.
In 2 dimensions, the honeycomb represents the triangular tiling, with Coxeter graph Template:CDD filling the plane with alternately colored triangles. In 3 dimensions it represents the tetrahedral-octahedral honeycomb, with Coxeter graph Template:CDD filling space with alternately tetrahedral and octahedral cells. In 4 dimensions it is called the 5-cell honeycomb, with Coxeter graph Template:CDD, with 5-cell and rectified 5-cell facets. In 5 dimensions it is called the 5-simplex honeycomb, with Coxeter graph Template:CDD, filling space by 5-simplex, rectified 5-simplex, and birectified 5-simplex facets. In 6 dimensions it is called the 6-simplex honeycomb, with Coxeter graph Template:CDD, filling space by 6-simplex, rectified 6-simplex, and birectified 6-simplex facets.
By dimension
Projection by folding
The (2n-1)-simplex honeycombs and 2n-simplex honeycombs can be projected into the n-dimensional hypercubic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:
Kissing number
These honeycombs, seen as tangent n-spheres located at the center of each honeycomb vertex have a fixed number of contacting spheres and correspond to the number of vertices in the vertex figure. For 2 and 3 dimensions, this represents the highest kissing number for 2 and 3 dimensions, but fall short on higher dimensions. In 2-dimensions, the triangular tiling defines a circle packing of 6 tangent spheres arranged in a regular hexagon, and for 3 dimensions there are 12 tangent spheres arranged in an cuboctahedral configuration. For 4 to 8 dimensions, the kissing numbers are 20, 30, 42, 56, and 72 spheres, while the greatest solutions are 24, 40, 72, 126, and 240 spheres respectively.
See also
- Hypercubic honeycomb
- Alternated hypercubic honeycomb
- Quarter hypercubic honeycomb
- Truncated simplectic honeycomb
- Omnitruncated simplectic honeycomb
References
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
(I'm no baseball guy, but if you increase the opponent's chance of winning by intentionally putting a runner on first in that situation, how come EVERY manager does it?
The citizens of Summerside and the surrounding area derserved this facility, for too long we had to use outdated decrepit, unsafe and embarassing facilities, I applaud ethe Mayor and the Council at the time who had the vision, and the and the community spirit to push the building of this facility thru all the politics and legal stuff to get this built. And it continues to grow, The addition of a the skateboarding facility tp CUP is proving to be a well used and appreciated park for our young citizens.
http://southfloridanfp.org/coach/?key=cheap-coach-outlet-24
http://southfloridanfp.org/coach/?key=coach-gilroy-outlet-90
http://southfloridanfp.org/coach/?key=coach-sneakers-outlet-25
http://southfloridanfp.org/coach/?key=coach-bags-on-sale-at-outlet-33
http://southfloridanfp.org/coach/?key=coach-pocketbooks-outlet-64
If you adored this post and you would certainly such as to receive additional facts concerning Cheap Uggs Boots kindly go to the web site.