Partial application: Difference between revisions
en>Mogism m Typo fixing and cleanup, typos fixed: libary → library, eg → e.g. using AWB |
fix paywalled link |
||
| Line 1: | Line 1: | ||
[[Image:Doubling oriented.svg|300px|right|thumb|A Doubling-oriented Doche-Icart-Kohel curve of equation <math>y^2=x^3-x^2-16x</math>]] | |||
In [[mathematics]], the '''doubling-oriented Doche–Icart–Kohel curve''' is a form in which an [[elliptic curve]] can be written. It is a special case of [[Weierstrass form]] and it is also important in [[elliptic curve cryptography|elliptic-curve cryptography]] because the doubling speeds up considerably (computing as composition of 2-[[isogeny]] and its [[dual abelian variety|dual]]). | |||
It has been introduced by Christophe Doche, Thomas Icart, and David R. Kohel in <ref>Christophe Doche, Thomas Icart, and David R. Kohel, ''Efficient Scalar Multiplication by Isogeny Decompositions''</ref> | |||
==Definition== | |||
Let <math> K </math> be a [[field (mathematics)|field]] and let <math>a\in K</math>. Then, the Doubling-oriented Doche–Icart–Kohel curve with [[parameter]] ''a'' in [[affine space|affine coordinates]] is represented by: | |||
<math> y^2=x^3+ax^2+16ax </math> | |||
Equivalently, in [[projective space|projective coordinates]]: | |||
<math> ZY^2=X^3+aZX^2+16aXZ^2, </math> | |||
with <math> x=\frac{X}{Z} </math> and <math>y=\frac{Y}{Z} </math>. | |||
Notice that, since this curve is a special case of [[elliptic curve|Weierstrass form]], transformations to the most common form of elliptic curve (Weierstrass form) are not needed. | |||
==Group law== | |||
It is interesting to analyze the [[elliptic curve#The group law|group law]] in [[elliptic curve cryptography]], defining the addition and doubling formulas, because these formulas are necessary to compute multiples of points ''[n]P'' (see [[Exponentiation by squaring]]). In general, the group law is defined in the following way: if three points lies in the same line then they sum up to zero. So, by this property, the group laws are different for every curve shape. | |||
In this case, since these curves are special cases of Weierstrass curves, the addition is just the standard addition on Weierstrass curves. On the other hand, to double a point, the standard doubling formula can be used, but it would not be so fast. | |||
In this case, the [[identity element|neutral element]] is <math> \theta=(0:1:0) </math> (in projective coordinates), for which <math> \theta=-\theta </math>. Then, if <math>P=(x,y)</math> is a non-trivial element (<math>P!=O</math>), then the inverse of this point (by addition) is –P=(x,-y). | |||
===Addition=== | |||
In this case, [[affine space|affine coordinates]] will be used to define the addition formula: | |||
(x<sub>1</sub>,y<sub>1</sub>)+(x<sub>2</sub>,y<sub>2</sub>)=(x<sub>3</sub>,y<sub>3</sub>) where | |||
x<sub>3</sub> = (-x<sub>1</sub><sup>3</sup>+(x<sub>2</sub>-a)x<sub>1</sub><sup>2</sup>+(x<sub>2</sub><sup>2</sup>+2ax<sub>2</sub>)x<sub>1</sub>+(y<sub>1</sub><sup>2</sup>-2y<sub>2</sub>y<sub>1</sub>+(-x<sub>2</sub><sup>3</sup>-ax<sub>2</sub><sup>2</sup>+y<sub>2</sub><sup>2</sup>)))/(x<sub>1</sub><sup>2</sup>-2x<sub>2</sub>x<sub>1</sub>+x<sub>2</sub><sup>2</sup>) | |||
y<sub>3</sub> = ((-y<sub>1</sub>+2y<sub>2</sub>)x<sub>1</sub><sup>3</sup>+(-ay<sub>1</sub>+(-3y<sub>2</sub>x<sub>2</sub>+ay<sub>2</sub>))x<sub>1</sub><sup>2</sup>+((3x<sub>2</sub><sup>2</sup>+2ax<sub>2</sub>)y<sub>1</sub>-2ay<sub>2</sub>x<sub>2</sub>)x<sub>1</sub>+(y<sub>1</sub><sup>3</sup>-3y<sub>2</sub>y<sub>1</sub><sup>2</sup>+(-2x<sub>2</sub><sup>3</sup>-ax<sub>2</sub><sup>2</sup>+3y<sub>2</sub><sup>2</sup>)y<sub>1</sub>+(y<sub>2</sub>x<sub>2</sub><sup>3</sup>+ay<sub>2</sub>x<sub>2</sub><sup>2</sup>-y<sub>2</sub><sup>3</sup>)))/(-x<sub>1</sub><sup>3</sup>+3x<sub>2</sub>x<sub>1</sub><sup>2</sup>-3x<sub>2</sub><sup>2</sup>x<sub>1</sub>+x<sub>2</sub><sup>3</sup>) | |||
===Doubling=== | |||
2(x<sub>1</sub>,y<sub>1</sub>)=(x<sub>3</sub>,y<sub>3</sub>) | |||
x<sub>3</sub> = 1/(4y<sub>1</sub><sup>2</sup>)x<sub>1</sub><sup>4</sup>-8a/y<sub>1</sub><sup>2</sup>x<sub>1</sub><sup>2</sup>+64a2/y<sub>1</sub><sup>2</sup> | |||
y<sub>3</sub> = 1/(8y<sub>1</sub><sup>3</sup>)x<sub>1</sub><sup>6</sup>+((-a<sup>2</sup>+40a)/(4y<sub>1</sub><sup>3</sup>))x<sub>1</sub><sup>4</sup>+((ay<sub>1</sub><sup>2</sup>+(16a<sup>3</sup>-640a<sup>2</sup>))/(4y<sub>1</sub><sup>3</sup>))x<sub>1</sub><sup>2</sup>+((-4a<sup>2</sup>y<sub>1</sub><sup>2</sup>-512a<sup>3</sup>)/y<sub>1</sub><sup>3</sup>) | |||
==Algorithms and examples== | |||
===Addition=== | |||
The fastest addition is the following one (comparing with the results given in: http://hyperelliptic.org/EFD/g1p/index.html), and the cost that it takes is 4 multiplications, 4 squaring and 10 addition. | |||
A = Y<sub>2</sub>-Y<sub>1</sub> | |||
AA = A<sup>2</sup> | |||
B = X<sub>2</sub>-X<sub>1</sub> | |||
CC = B<sup>2</sup> | |||
F = X<sub>1</sub>CC | |||
Z<sub>3</sub> = 2CC | |||
D = X<sub>2</sub>Z<sub>3</sub> | |||
ZZ<sub>3</sub> = Z<sub>3</sub><sup>2</sup> | |||
X<sub>3</sub> = 2(AA-F)-aZ<sub>3</sub>-D | |||
Y<sub>3</sub> = ((A+B)<sup>2</sup>-AA-CC)(D-X<sub>3</sub>)-Y<sub>2</sub>ZZ<sub>3</sub> | |||
====Example==== | |||
Let <math> K=\mathbb{Q} </math>. Let P=(X<sub>1</sub>,Y<sub>1</sub>)=(2,1), Q=(X<sub>2</sub>,Y<sub>2</sub>)=(1,-1) and a=1, then | |||
A=2 | |||
AA=4 | |||
B=1 | |||
CC=1 | |||
F=2 | |||
''' Z<sub>3</sub>=4''' | |||
D=4 | |||
ZZ<sub>3</sub>=16 | |||
''' X<sub>3</sub>=-4''' | |||
'''Y<sub>3</sub>=336 ''' | |||
Thus, P+Q=(-4:336:4) | |||
===Doubling=== | |||
The following algorithm is the fastest one (see the following link to compare: http://hyperelliptic.org/EFD/g1p/index.html), and the cost that it takes is 1 multiplication, 5 squaring and 7 additions. | |||
A = X<sub>1</sub><sup>2</sup> | |||
B = A-a16 | |||
C = a<sub>2</sub>A | |||
YY = Y<sub>1</sub><sup>2</sup> | |||
YY<sub>2</sub> = 2YY | |||
Z<sub>3</sub> = 2YY<sub>2</sub> | |||
X<sub>3</sub> = B<sup>2</sup> | |||
V = (Y<sub>1</sub>+B)2-YY-X<sub>3</sub> | |||
Y<sub>3</sub> = V(X<sub>3</sub>+64C+a(YY<sub>2</sub>-C)) | |||
ZZ<sub>3</sub> = Z<sub>3</sub><sup>2</sup> | |||
====Example==== | |||
Let <math> K=\mathbb{Q} </math> and a=1. Let P=(-1,2), then Q=[2]P=(x3,y3) is given by: | |||
A=1 | |||
B=-15 | |||
C=2 | |||
YY=4 | |||
YY<sub>2</sub>=8 | |||
'''Z<sub>3</sub>=16''' | |||
'''X<sub>3</sub>=225''' | |||
V=27 | |||
'''Y<sub>3</sub>=9693''' | |||
ZZ<sub>3</sub>=256 | |||
Thus, Q=(225:9693:16). | |||
==Extended coordinates== | |||
The addition and doubling computations should be as fast as possible, so it is more convenient to use the following representation of the coordinates: | |||
<math> x,y </math> are represented by <math> X,Y,Z,ZZ </math> satisfying the following equations: | |||
<math> x=\frac{X}{Z} </math> | |||
<math> y=\frac{Y}{ZZ} </math> | |||
<math> ZZ=Z^2 </math> | |||
Then, the Doubling-oriented Doche–Icart–Kohel curve is given by the following equation: | |||
<math> Y^2=ZX^3+aZ^2X^2+16aZ^3X </math>. | |||
In this case,<math> P=(X: Y: Z: ZZ)</math> is a general point with inverse <math>-P=(X: -Y: Z: ZZ) </math>. | |||
Furthermore, the points over the curve satisfy: <math> (X:Y:Z:Z^2)=(\lambda X: \lambda^2Y: \lambda Z: \lambda^2Z^2) </math> for all <math> \lambda </math> nonzero. | |||
Faster doubling formulas for these curves and mixed-addition formulas were introduced by Doche, Icart and Kohel; but nowadays, these formulas are improved by Daniel J. Bernstein and Tanja Lange (see below the link of EFD). | |||
==Internal Link== | |||
For more informations about the running-time required in a specific case, see [[Table of costs of operations in elliptic curves]] | |||
==External links== | |||
* http://hyperelliptic.org/EFD/g1p/index.html | |||
==Notes== | |||
{{Reflist}} | |||
==References== | |||
* {{cite book | |||
| author = Christophe Doche, Thomas Icart and David R. Kohel | |||
| year = 2006 | |||
| title = Efficient Scalar Multiplication by Isogeny Decompositions | |||
| publisher =Springer Berlin / Heidelberg | |||
| url = http://www.springerlink.com/content/h542176232q8w45q/fulltext.pdf | |||
| isbn = 978-3-540-33851-2 | |||
}} | |||
* {{cite book | |||
| author = Daniel J. Bernstein and Tanja Lange | |||
| year = 2008 | |||
| title = Analysis and optimization of elliptic-curve single scalar multiplication | |||
| publisher = | |||
| url = http://books.google.nl/books?hl=es&lr=&id=VZ5kFYzH_ZUC&oi=fnd&pg=PA1&dq=related:0lMQ2OY5ejoJ:scholar.google.com/&ots=7erHZiu8CS&sig=PJCJlQQIhvqu0njfTyaV4DLYlkg#v=onepage&q=&f=false | |||
| isbn = | |||
}} | |||
* http://www.hyperelliptic.org/EFD/g1p/auto-2dik.html | |||
{{DEFAULTSORT:Doubling-oriented Doche-Icart-Kohel curve}} | |||
[[Category:Elliptic curves]] | |||
[[Category:Elliptic curve cryptography]] | |||
Revision as of 02:01, 5 October 2013
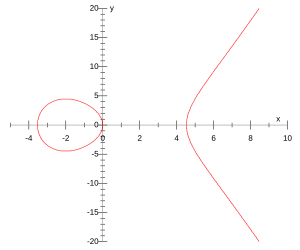
In mathematics, the doubling-oriented Doche–Icart–Kohel curve is a form in which an elliptic curve can be written. It is a special case of Weierstrass form and it is also important in elliptic-curve cryptography because the doubling speeds up considerably (computing as composition of 2-isogeny and its dual). It has been introduced by Christophe Doche, Thomas Icart, and David R. Kohel in [1]
Definition
Let be a field and let . Then, the Doubling-oriented Doche–Icart–Kohel curve with parameter a in affine coordinates is represented by:
Equivalently, in projective coordinates:
Notice that, since this curve is a special case of Weierstrass form, transformations to the most common form of elliptic curve (Weierstrass form) are not needed.
Group law
It is interesting to analyze the group law in elliptic curve cryptography, defining the addition and doubling formulas, because these formulas are necessary to compute multiples of points [n]P (see Exponentiation by squaring). In general, the group law is defined in the following way: if three points lies in the same line then they sum up to zero. So, by this property, the group laws are different for every curve shape.
In this case, since these curves are special cases of Weierstrass curves, the addition is just the standard addition on Weierstrass curves. On the other hand, to double a point, the standard doubling formula can be used, but it would not be so fast. In this case, the neutral element is (in projective coordinates), for which . Then, if is a non-trivial element (), then the inverse of this point (by addition) is –P=(x,-y).
Addition
In this case, affine coordinates will be used to define the addition formula:
(x1,y1)+(x2,y2)=(x3,y3) where
x3 = (-x13+(x2-a)x12+(x22+2ax2)x1+(y12-2y2y1+(-x23-ax22+y22)))/(x12-2x2x1+x22)
y3 = ((-y1+2y2)x13+(-ay1+(-3y2x2+ay2))x12+((3x22+2ax2)y1-2ay2x2)x1+(y13-3y2y12+(-2x23-ax22+3y22)y1+(y2x23+ay2x22-y23)))/(-x13+3x2x12-3x22x1+x23)
Doubling
2(x1,y1)=(x3,y3)
x3 = 1/(4y12)x14-8a/y12x12+64a2/y12
y3 = 1/(8y13)x16+((-a2+40a)/(4y13))x14+((ay12+(16a3-640a2))/(4y13))x12+((-4a2y12-512a3)/y13)
Algorithms and examples
Addition
The fastest addition is the following one (comparing with the results given in: http://hyperelliptic.org/EFD/g1p/index.html), and the cost that it takes is 4 multiplications, 4 squaring and 10 addition.
A = Y2-Y1
AA = A2
B = X2-X1
CC = B2
F = X1CC
Z3 = 2CC
D = X2Z3
ZZ3 = Z32
X3 = 2(AA-F)-aZ3-D
Y3 = ((A+B)2-AA-CC)(D-X3)-Y2ZZ3
Example
Let . Let P=(X1,Y1)=(2,1), Q=(X2,Y2)=(1,-1) and a=1, then
A=2
AA=4
B=1
CC=1
F=2
Z3=4
D=4
ZZ3=16
X3=-4
Y3=336
Thus, P+Q=(-4:336:4)
Doubling
The following algorithm is the fastest one (see the following link to compare: http://hyperelliptic.org/EFD/g1p/index.html), and the cost that it takes is 1 multiplication, 5 squaring and 7 additions.
A = X12
B = A-a16
C = a2A
YY = Y12
YY2 = 2YY
Z3 = 2YY2
X3 = B2
V = (Y1+B)2-YY-X3
Y3 = V(X3+64C+a(YY2-C))
ZZ3 = Z32
Example
Let and a=1. Let P=(-1,2), then Q=[2]P=(x3,y3) is given by:
A=1
B=-15
C=2
YY=4
YY2=8
Z3=16
X3=225
V=27
Y3=9693
ZZ3=256
Thus, Q=(225:9693:16).
Extended coordinates
The addition and doubling computations should be as fast as possible, so it is more convenient to use the following representation of the coordinates:
are represented by satisfying the following equations:
Then, the Doubling-oriented Doche–Icart–Kohel curve is given by the following equation:
In this case, is a general point with inverse . Furthermore, the points over the curve satisfy: for all nonzero.
Faster doubling formulas for these curves and mixed-addition formulas were introduced by Doche, Icart and Kohel; but nowadays, these formulas are improved by Daniel J. Bernstein and Tanja Lange (see below the link of EFD).
Internal Link
For more informations about the running-time required in a specific case, see Table of costs of operations in elliptic curves
External links
Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - http://www.hyperelliptic.org/EFD/g1p/auto-2dik.html
- ↑ Christophe Doche, Thomas Icart, and David R. Kohel, Efficient Scalar Multiplication by Isogeny Decompositions




















