Analyst's traveling salesman theorem: Difference between revisions
en>JustAGal Disambiguated: Peter Jones → Peter Jones (mathematician) |
en>Bgwhite m Checking Wikipedia using AutoEd |
||
| Line 1: | Line 1: | ||
{{original research|date=August 2010}} | |||
The '''Miller theorem''' refers to the process of creating [[equivalent circuit]]s. It asserts that a floating impedance element, supplied by two voltage sources connected in series, may be split into two grounded elements with corresponding impedances. There is also a [[#Dual Miller theorem|dual Miller theorem]] with regards to impedance supplied by two current sources connected in parallel. The two versions are based on the two [[Kirchhoff's circuit laws]]. | |||
Miller theorems are not only pure mathematical expressions. These arrangements explain important circuit phenomena about modifying impedance ([[Miller effect]], [[virtual ground]], [[Bootstrapping (electronics)|bootstrapping]], [[negative impedance]], etc.) and help in designing and understanding various commonplace circuits (feedback amplifiers, resistive and time-dependent converters, negative impedance converters, etc.). The theorems are useful in 'circuit analysis' especially for analyzing circuits with feedback<ref name = "netlecturer">{{cite web|url=http://www.netlecturer.com/NTOnLine/T08_THEOREMS/p06MiscTheorems.htm#G7 |title=Miscellaneous network theorems |publisher=Netlecturer.com |date= |accessdate=2013-02-03}}</ref> and certain transistor amplifiers at high frequencies.<ref name = "sandiego">{{cite web|url=http://home.sandiego.edu/~ekim/e194rfs01/millers.pdf |title=EEE 194RF: Miller's theorem |format=PDF |date= |accessdate=2013-02-03}}</ref> | |||
There is a close relationship between Miller theorem and Miller effect: the theorem may be considered as a generalization of the effect and the effect may be thought as of a special case of the theorem. | |||
== Miller theorem (for voltages) == | |||
=== Definition === | |||
The Miller theorem establishes that in a linear circuit, if there exists a branch with impedance ''Z'', connecting two nodes with nodal voltages ''V<sub>1</sub>'' and ''V<sub>2</sub>'', we can replace this branch by two branches connecting the corresponding nodes to ground by impedances respectively Z/(1 − K) and KZ/(K − 1), where K = V<sub>2</sub>/V<sub>1</sub>. The Miller theorem may be proved by using the equivalent two-port network technique to replace the two-port to its equivalent and by applying the source absorption theorem.<ref name = "paginas">{{cite web|url=http://paginas.fe.up.pt/~fff/eBook/MDA/Teo_Miller.html |title=Miller's theorem |publisher=Paginas.fe.up.pt |date= |accessdate=2013-02-03}}</ref> This version of the Miller theorem is based on [[Kirchhoff's voltage law]]; for that reason, it is named also ''Miller theorem for voltages''. | |||
=== Explanation === | |||
Miller theorem implies that an impedance element is supplied by two arbitrary (not necessarily dependent) voltage sources that are connected in series through the common ground. In practice, one of them acts as a main (independent) voltage source with voltage ''V<sub>1</sub>'' and the other – as an additional (linearly dependent) voltage source with voltage <math>V_2 = K{V_1}</math>. The idea of Miller theorem (modifying circuit impedances seen from the sides of the input and output sources) is revealed below by comparing the two situations – without and with connecting an additional voltage source V<sub>2</sub>. | |||
If ''V<sub>2</sub>'' was zero (there was not a second voltage source or the right end of the element with impedance ''Z'' was just grounded), the input current flowing through the element would be determined, according to Ohm's law, only by ''V<sub>1</sub>'' | |||
:<math>I_{in0} = \frac{V_1}{Z}</math> | |||
and the input impedance of the circuit would be | |||
:<math>Z_{in0} = \frac{V_1}{I_{in0}} = Z.</math> | |||
As a second voltage source is included, the input current depends on both the voltages. According to its polarity, ''V<sub>2</sub>'' is subtracted from or added to ''V<sub>1</sub>''; so, the input current decreases/increases | |||
:<math>I_{in} = \frac{V_1 - V_2}{Z} = \frac{(1 - K)}{Z}{V_1} = {(1 - K)}{I_{in0}}</math> | |||
and the input impedance of the circuit seen from the side of the input source accordingly increases/decreases | |||
:<math>Z_{in} = \frac{V_1}{I_{in}} = \frac{Z}{1-K}.</math> | |||
So, Miller theorem expresses the fact that '''''connecting a second voltage source with proportional voltage <math>V_2 = K{V_1}</math> in series with the input voltage source changes the effective voltage, the current and respectively, the circuit impedance seen from the side of the input source'''''. Depending on the polarity, ''V<sub>2</sub>'' acts as a supplemental voltage source helping or opposing the main voltage source to pass the current through the impedance. | |||
Besides by presenting the combination of the two voltage sources as a new composed voltage source, the theorem may be explained by ''combining the actual element and the second voltage source into a new virtual element with dynamically modified impedance''. From this viewpoint, ''V<sub>2</sub>'' is an additional voltage that artificially increases/decreases the voltage drop ''V<sub>z</sub>'' across the impedance ''Z'' thus decreasing/increasing the current. The proportion between the voltages determines the value of the obtained impedance (see the tables below) and gives in total six groups of typical [[#Applications|applications]]. | |||
{| border="1" | |||
|+'''Subtracting ''V<sub>2</sub>'' from ''V<sub>1</sub>''''' | |||
|- | |||
|<center>'''''V<sub>2</sub>'' vs ''V<sub>1</sub>'''''</center>||<center>'''''V<sub>2</sub>'' = 0'''</center>||<center>'''0 < ''V<sub>2</sub>'' < ''V<sub>1</sub>'''''</center>||<center>'''''V<sub>2</sub>'' = ''V<sub>1</sub>'''''</center>||<center>'''''V<sub>2</sub>'' > ''V<sub>1</sub>'''''</center> | |||
|- | |||
|<center>'''Impedance'''<center>||<center>normal</center>||<center>increased</center>||<center>infinite</center>||<center>negative with current inversion</center> | |||
|} | |||
{| border="1" | |||
|+'''Adding ''V<sub>2</sub>'' to ''V<sub>1</sub>''''' | |||
|- | |||
|<center>'''''V<sub>2</sub>'' vs ''V<sub>z</sub>'''''</center>||<center>'''''V<sub>2</sub>'' = 0'''</center>||<center>'''0 < ''V<sub>2</sub>'' < ''V<sub>z</sub>'''''</center>||<center>'''''V<sub>2</sub>'' = ''V<sub>z</sub>'''''</center>||<center>'''''V<sub>2</sub>'' > ''V<sub>z</sub>'''''</center> | |||
|- | |||
|<center>'''Impedance'''<center>||<center>normal</center>||<center>decreased</center>||<center>zero</center>||<center>negative with voltage inversion</center> | |||
|} | |||
The circuit impedance, seen from the side of the output source, may be defined similarly, if the voltages ''V<sub>1</sub>'' and ''V<sub>2</sub>'' are swapped and the coefficient ''K'' is replaced by 1/''K'' | |||
:<math>Z_{in2} = \frac{{K}{Z}}{K-1}.</math> | |||
=== Implementation === | |||
[[Image:Miller cir.png|right|frame|A typical implementation of Miller theorem based on a single-ended voltage amplifier]] | |||
Most frequently, the Miller theorem may be observed in, and implemented by, an arrangement consisting of an element with impedance ''Z'' connected between the two terminals of a grounded general linear network.<ref name="sandiego"/> Usually, a voltage amplifier with gain of <math>A_V = K</math> serves as such a linear network, but also other devices can play this role: a man and a [[potentiometer]] in a [[Potentiometer (measuring instrument)#Constant current potentiometer|potentiometric null-balance meter]], an electromechanical integrator (servomechanisms using potentiometric feedback sensors), etc. | |||
In the amplifier implementation, the input voltage ''V<sub>i</sub>'' serves as ''V<sub>1</sub>'' and the output voltage ''V<sub>o</sub>'' – as ''V<sub>2</sub>''. In many cases, the input voltage source has some internal impedance <math>Z_{int}</math> or an additional input impedance is connected that, in combination with ''Z'', introduces a feedback. Depending on the kind of amplifier (non-inverting, inverting or differential), the feedback can be positive, negative or mixed. | |||
The Miller amplifier arrangement has two aspects: | |||
*the amplifier may be thought as an additional voltage source converting the actual impedance into a ''virtual impedance'' (the amplifier modifies the impedance of the actual element) | |||
* the virtual impedance may be thought as an element connected in parallel to the amplifier input (the virtual impedance modifies the amplifier input impedance). | |||
=== Applications === | |||
The introduction of an impedance that connects amplifier input and output ports adds a great | |||
deal of complexity in the analysis process. Miller theorem helps reduce the | |||
complexity in some circuits particularly with feedback<ref name = "sandiego" /> by converting them to simpler equivalent circuits. But Miller theorem is not only an effective tool for creating equivalent circuits; it is also a powerful tool for designing and understanding circuits based on ''modifying impedance by additional voltage''. Depending on the polarity of the output voltage versus the input voltage and the proportion between their magnitudes, there are six groups of typical situations. In some of them, the Miller phenomenon appears as desired ([[Bootstrapping (electronics)|bootstrapping]]) or undesired ([[Miller effect]]) unintentional effects; in other cases it is intentionally introduced. | |||
==== Applications based on subtracting ''V<sub>2</sub>'' from ''V<sub>1</sub> ==== | |||
In these applications, the output voltage ''V<sub>o</sub>'' is inserted with an opposite polarity in respect to the input voltage ''V<sub>i</sub>'' travelling along the loop (but in respect to ground, the polarities are the same). As a result, the effective voltage across, and the current through, the impedance decrease; the input impedance increases. | |||
{{anchor|increased}}'''Increased impedance''' is implemented by a non-inverting amplifier with gain of 0 < A<sub>v</sub> < 1. The (magnitude of) output voltage is less than the input voltage ''V<sub>i</sub>'' and partially neutralizes it. Examples are imperfect voltage followers ([[Emitter follower|emitter]], [[Source follower|source]], [[Cathode follower|cathode]] follower, etc.) and amplifiers with series negative feedback ([[Common emitter#Emitter degeneration|emitter degeneration]]), whose input impedance is moderately increased. | |||
[[Image:Op-Amp Non-Inverting Amplifier.svg|right|frame|The op-amp non-inverting amplifier is a typical circuit with series negative feedback based on the Miller theorem, where the op-amp differential input impedance is apparently increased up to infinite]] | |||
{{anchor|infinite}}'''Infinite impedance''' uses a non-inverting amplifier with A<sub>v</sub> = 1. The output voltage is equal to the input voltage ''V<sub>i</sub>'' and completely neutralizes it. Examples are [[Potentiometer (measuring instrument)#Constant current potentiometer|potentiometric null-balance meters]] and op-amp followers and amplifiers with series negative feedback ([[Voltage buffer|op-amp follower]] and [[Operational amplifier applications#Non-inverting amplifier|non-inverting amplifier]]) where the circuit input impedance is enormously increased. This technique is referred to as [[Bootstrapping (electronics)|bootstrapping]] and is intentionally used in biasing circuits, input guarding circuits,<ref>[http://www.national.com/an/AN/AN-241.pdf Working with High Impedance Op Amps] AN-241</ref> etc. | |||
{{anchor|negative current inversion}}'''Negative impedance obtained by current inversion''' is implemented by a non-inverting amplifier with A<sub>v</sub> > 1. The current changes its direction, as the output voltage is higher than the input voltage. If the input voltage source has some internal impedance <math>Z_{int}</math> or if it is connected through another impedance element, a positive feedback appears. A typical application is the [[Negative impedance converter|negative impedance converter with current inversion]] (INIC) that uses both negative and positive feedback (the negative feedback is used to realize a non-inverting amplifier and the positive feedback – to modify the impedance). | |||
==== Applications based on adding ''V<sub>2</sub>'' to ''V<sub>1</sub> ==== | |||
In these applications, the output voltage ''V<sub>o</sub>'' is inserted with the same polarity in respect to the input voltage ''V<sub>i</sub>'' travelling along the loop (but in respect to ground, the polarities are opposite). As a result, the effective voltage across and the current through the impedance increase; the input impedance decreases. | |||
{{anchor|decreased}}'''Decreased impedance''' is implemented by an inverting amplifier having some moderate gain, usually 10 < A<sub>v</sub> < 1000. It may be observed as an undesired [[Miller effect]] in [[common-emitter]], [[common-source]] and ''common-cathode'' amplifying stages where effective input capacitance is increased. [[Frequency compensation#Dominant-pole compensation|Frequency compensation]] for general purpose operational amplifiers and [http://books.google.bg/books?id=mfec2Zw_b7wC&pg=PA284&lpg=PA284&dq=%22transistor+Miller+integrator+%22&source=bl&ots=-8PdcUw4LD&sig=zOjnF9O-oUBjw0bU9a_SMYdgCYY&hl=en&ei=C7yMTIDjGM7Oswb3oLy7Ag&sa=X&oi=book_result&ct=result&resnum=4&ved=0CBsQ6AEwAw#v=onepage&q=%22transistor%20Miller%20integrator%20%22&f=false transistor Miller integrator] are examples of useful usage of the Miller effect. | |||
[[Image:Op-Amp Inverting Amplifier.svg|right|frame|The op-amp inverting amplifier is a typical circuit, with parallel negative feedback, based on the Miller theorem, where the op-amp differential input impedance is apparently decreased up to zero]] | |||
{{anchor|zeroed}}'''Zeroed impedance''' uses an inverting (usually op-amp) amplifier with enormously high gain A<sub>v</sub> → ∞. The output voltage is almost equal to the voltage drop ''V<sub>Z</sub>'' across the impedance and completely neutralizes it. The circuit behaves as a short connection and a [[virtual ground]] appears at the input; so, it should not be driven by a constant voltage source. For this purpose, some circuits are driven by a constant current source or by a real voltage source with internal impedance: [[current-to-voltage converter]] (transimpedance amplifier), capacitive integrator (named also [[current integrator]] or [[charge amplifier]]), resistance-to-voltage converter (a resistive sensor connected in the place of the impedance ''Z''). | |||
The rest of them have additional impedance connected in series to the input: [[voltage-to-current converter]] (transconductance amplifier), [[inverting amplifier]], [[summing amplifier]], inductive integrator, capacitive differentiator, [[Operational amplifier applications#Inverting integrator|resistive-capacitive integrator]], [[Operational amplifier applications#Inverting differentiator|capacitive-resistive differentiator]], inductive-resistive differentiator, etc. The inverting integrators from this list are examples of useful and desired applications of the Miller effect in its extreme manifestation. | |||
In all these ''op-amp inverting circuits with parallel negative feedback'', the input current is increased to its maximum. It is determined only by the input voltage and the input impedance according to [[Ohm's law]]; it does not depend on the impedance ''Z''. | |||
{{anchor|negative with voltage inversion}}'''Negative impedance with voltage inversion''' is implemented by applying both negative and positive feedback to an op-amp amplifier with a differential input. The input voltage source has to have internal impedance <math>Z_{int}</math> > 0 or it has to be connected through another impedance element to the input. Under these conditions, the input voltage ''V<sub>i</sub>'' of the circuit changes its polarity as the output voltage exceeds the voltage drop ''V<sub>Z</sub>'' across the impedance (''V<sub>i</sub>'' = ''V<sub>z</sub>'' – ''V<sub>o</sub>'' < 0). | |||
A typical application is a negative impedance converter with voltage inversion (VNIC).<ref>{{cite web|url=http://nonlinear.eecs.berkeley.edu/chaos/introduction_nonlinear_circuit_analysis.pdf |title=Nonlinear Circuit Analysis – An Introduction |format=PDF |date= |accessdate=2013-02-03}}</ref> It is interesting that the circuit input voltage has the same polarity as the output voltage, although it is applied to the inverting op-amp input; the input source has an opposite polarity to both the circuit input and output voltages. | |||
=== Generalization of Miller arrangement === | |||
The original Miller effect is implemented by capacitive impedance connected between the two nodes. Miller theorem generalizes Miller effect as it implies arbitrary impedance Z connected between the nodes. It is supposed also a constant coefficient K; then the expressions [[#Explanation|above]] are valid. But modifying properties of Miller theorem exist even when these requirements are violated and this arrangement can be generalized further by dynamizing the impedance and the coefficient. | |||
'''Non-linear element.''' Besides impedance, Miller arrangement can modify the IV characteristic of an arbitrary element. The circuit of a [[Operational amplifier applications#Logarithmic output|diode log converter]] is an example of a non-linear [[#zeroed|virtually zeroed resistance]] where the logarithmic [[diode#Current–voltage characteristic|forward IV curve of a diode]] is transformed to a vertical straight line overlapping the Y axis. | |||
'''Not constant coefficient.''' If the coefficient K varies, some exotic virtual elements can be obtained. A [[Gyrator#Implementation: a simulated inductor|gyrator circuit]] is an example of such a virtual element where the resistance R<sub>L</sub> is modified so that to mimic inductance, capacitance or inversed resistance. | |||
== Dual Miller theorem (for currents) == | |||
=== Definition === | |||
There is also a dual version of Miller theorem that is based on [[Kirchhoff's current law]] (''Miller theorem for currents''): if there is a branch in a circuit with impedance Z connecting a node, where two currents I<sub>1</sub> and I<sub>2</sub> converge to ground, we can replace this branch by two conducting the referred currents, with impedances respectively equal to (1 + α)Z and (1 + α)Z/α, where α = I<sub>2</sub>/I<sub>1</sub>. The dual theorem may be proved by replacing the two-port network by its equivalent and by applying the source absorption theorem.<ref name = "paginas" /> | |||
=== Explanation === | |||
Dual Miller theorem actually expresses the fact that '''''connecting a second current source producing proportional current <math>I_2 = K{I_1}</math> in parallel with the main input source and the impedance element changes the current flowing through it, the voltage and accordingly, the circuit impedance seen from the side of the input source'''''. Depending on the direction, ''I<sub>2</sub>'' acts as a supplemental current source helping or opposing the main current source ''I<sub>1</sub>'' to create voltage across the impedance. The combination of the actual element and the second current source may be thought as of a new virtual element with dynamically modified impedance. | |||
=== Implementation === | |||
Dual Miller theorem is usually implemented by an arrangement consisting of two voltage sources supplying the grounded impedance ''Z'' through floating impedances (see [http://www.maxim-ic.com/app-notes/index.mvp/id/1155 Fig. 3]). The combinations of the voltage sources and belonging impedances form the two current sources – the main and the auxiliary one. As in the case of the main Miller theorem, the second voltage is usually produced by a voltage amplifier. Depending on the kind of the amplifier (inverting, non-inverting or differential) and the gain, the circuit input impedance may be virtually increased, infinite, decreased, zero or negative. | |||
=== Applications === | |||
As the main Miller theorem, besides helping circuit analysis process, the dual version is a powerful tool for designing and understanding circuits based on modifying impedance by additional current. Typical applications are some exotic circuits with negative impedance as load cancellers,<ref name="load caceller">[http://www.elecdesign.com/Articles/Index.cfm?AD=1&ArticleID=4128 Negative-resistance load canceller helps drive heavy loads]</ref> capacitance neutralizers,<ref>[http://www.philbrickarchive.org/1964-1_v12_no1_the_lightning_empiricist.htm Impedance and admittance transformations using operational amplifiers] by D. H. Sheingold</ref> Howland current source and its derivative Deboo integrator.<ref>{{cite web|url=http://www.maxim-ic.com/app-notes/index.mvp/id/1155 |title=Consider the "Deboo" Single-Supply Integrator |publisher=Maxim-ic.com |date=2002-08-29 |accessdate=2013-02-03}}</ref> In the last example (see Fig. 1 there), the Howland current source consists of an input voltage source V<sub>IN</sub>, a positive resistor R, a load (the capacitor C acting as impedance ''Z'') and a negative impedance converter INIC (R<sub>1</sub> = R<sub>2</sub> = R<sub>3</sub> = R and the op-amp). The input voltage source and the resistor R constitute an imperfect current source passing current ''I<sub>R</sub>'' through the load (see Fig. 3 in the source). The INIC acts as a second current source passing "helping" current ''I<sub>-R</sub>'' through the load. As a result, the total current flowing through the load is constant and the circuit impedance seen by the input source is increased. As a comparison, in a [http://www.elecdesign.com/Articles/Index.cfm?AD=1&ArticleID=4128 load canceller], the INIC passes all the required current through the load; the circuit impedance seen from the side of the input source (the load impedance) is almost infinite. | |||
== List of specific applications based on Miller theorems == | |||
Below is a list of circuit solutions, phenomena and techniques based on the two Miller theorems. | |||
{{hidden begin|toggle=left|title=Circuit solutions|titlestyle=padding-left: 4em;}} | |||
* Potentiometric null-balance meter | |||
* Electromechanical data recorders with a potentiometric servo system | |||
* Emitter (source, cathode) follower | |||
* Transistor amplifier with emitter (source, cathode) degeneration | |||
* Transistor bootstrapped biasing circuits | |||
* Transistor integrator | |||
* Common-emitter (common-source, common-cathode) amplifying stages with stray capacitances | |||
* Op-amp follower | |||
* Op-amp non-inverting amplifier | |||
* Op-amp bootstrapped AC follower with high input impedance | |||
* Bilateral current source | |||
* Negative impedance converter with current inversion (INIC) | |||
* Negative impedance load canceller | |||
* Negative impedance input capacitance canceller | |||
* Howland current source | |||
* Deboo integrator | |||
* Op-amp inverting ammeter | |||
* Op-amp voltage-to-current converter (transconductance amplifier) | |||
* Op-amp current-to-voltage converter (transimpedance amplifier) | |||
* Op-amp resistance-to-current converter | |||
* Op-amp resistance-to-voltage converter | |||
* Op-amp inverting amplifier | |||
* Op-amp inverting summer | |||
* Op-amp inverting capacitive integrator (current integrator, charge amplifier) | |||
* Op-amp inverting resistive-capacitive integrator | |||
* Op-amp inverting capacitive differentiator | |||
* Op-amp inverting capacitive-resistive differentiator | |||
* Op-amp inverting inductive integrator | |||
* Op-amp inverting inductive-resistive differentiator, etc. | |||
* Op-amp diode log converter | |||
* Op-amp diode anti-log converter | |||
* Op-amp inverting diode limiter (precision diode) | |||
* Negative impedance converter with voltage inversion (VNIC), etc. | |||
{{hidden end}} | |||
{{hidden begin|toggle=left|title=Circuit phenomena and techniques|titlestyle=padding-left: 4em;}} | |||
* Bootstrapping | |||
* Input guarding of high impedance op-amp circuits | |||
* Input-capacitance neutralization | |||
* Virtual ground | |||
* Miller effect | |||
* Frequency op-amp compensation | |||
* Negative impedance | |||
* Load cancelling | |||
{{hidden end}} | |||
== See also == | |||
*[[Miller effect]] | |||
*[[Negative feedback amplifier]] | |||
*[[Operational amplifier applications]] | |||
*[[Bootstrapping (electronics)#Amplifiers|Bootstrapping]] | |||
== References == | |||
<references/> | |||
== External links == | |||
* [http://www.springerlink.com/content/p588u5532kk44t13/ Miller's theorem revisited] | |||
* [http://www.springerlink.com/content/d63h832p1q7hk118/ New Results Related to Miller’s Theorem] | |||
* [http://ieeexplore.ieee.org/Xplore/login.jsp?url=http%3A%2F%2Fieeexplore.ieee.org%2Fiel1%2F13%2F497%2F00009752.pdf%3Farnumber%3D9752&authDecision=-203 A network theorem dual to Miller's theorem] | |||
* [http://sciencestage.com/d/4200272/generalized-miller-theorem-and-its-applications.html Generalized Miller theorem and its applications] | |||
* [http://www.tandfonline.com/doi/abs/10.1080/002072198133860 The Feedback Decomposition Theorem (FDT): The evolution of Miller's Theorem] | |||
* [http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1495756&tag=1 An Accurate Calculation of Miller Effect on the Frequency Response and on the Input and Output Impedances of Feedback Amplifiers (using FDT)] | |||
== Further reading == | |||
*''Fundamentals of Microelectronics'' by Behzad Razavi | |||
*''Microelectronic Circuits'' by Adel Sedra and Kenneth Smith | |||
*''Fundamentals of RF Circuit Design'' by Jeremy Everard | |||
[[Category:Electrical engineering]] | |||
[[Category:Electronic design]] | |||
[[Category:Analog circuits]] | |||
[[Category:Circuit theorems]] | |||
Revision as of 01:54, 12 September 2012
Picking the right webhosting service is vital. The last thing you wish to do is get a website released with a hosting service (after discovering to utilize that hosting service), then be disappointed with the service and need to mess around with moving your website to another hosting service.
I'm a delighted HostGator client. I utilize both HostGator and Bluehost. I suggest both. This short article is a thorough HostGator evaluation.
I'll begin with among the most important considerations: Cost
HostGator has several rates plans. They are as follows (since the date this short article was released):.
Hatchling Strategy: as low as $4.95 per month with a 3 year commitment. On this plan you can host one website.
Baby Plan: as reduced as $7.95 per month with a 3 year dedication. On this plan you can host an endless variety of websites.
Business Strategy: as reduced as $12.95 per month with 3 year commitment.
You do not need to commit for 3 years. With much shorter term commitments, you'll pay somewhat more per month.
You can likewise get your own specialized server if this is something you like to have.
If you loved this article and also you would like to obtain more info concerning http://www.hostgator1centcoupon.info/ i implore you to visit our own web site. Limitless variety of websites.
I wouldn't think about a hosting service that didn't let me host an unrestricted variety of websites for one regular monthly price under $10. I have numerous sites and I such as the versatility of having the ability to construct more websites at no added expense (except for signing up the domain).
If you go with the Infant Plan (this is the strategy I have) or Business Strategy, you can host as numerous websites on as numerous domain names as you like. This is where making use of a hosting service like HostGator can conserve you a lot of cash in the long run against making use of a website builder or having a website designer host your websites. When you utilize a website builder or have a website designer host your site, you'll normally pay additional for each extra site (or each added set of websites).
The disadvantage obviously, is you must handle your very own hosting. Nevertheless, luckily, this isn't really tough with the user friendly CPanel and technical support.
Domain registration.
You can easily register domain names with HostGator. You have to spend for each domain. REMEMBER to set your domain names on auto-renew (and that your billing details is set up to auto-pay) so your domain name registration does not lapse. Absolutely nothing can be worse than developing a terrific internet site and afterwards to lose it all due to the fact that you forgot to renew your domain name. It's possible then that somebody else registers your domain and you cannot get it once again. That might be devastating.
All HostGator prepares offer unrestricted bandwidth.
This is great and you ought to require this with any website hosting service. I would rule out using a hosting service that didn't provide unlimited bandwidth.
Simple CPanel Control panel.
You manage your sites with HostGator in a control panel referred to as a CPanel. The CPanel is an easy-to-use user interface to manage your sites and domains.
Easy website setup.
I specifically require with any hosting service that I utilize can set up WordPress with practically a single click or a series of simple clicks. HostGator provides Fantastico De Luxe and QuickInstall choices for easily setting up WordPress and many other scripts to develop your site (i.e. Joomla and others).
Access to 4,500 website design templates.
For any internet designer, this is huge. This is a fantastic way to develop websites inexpensively for customers. You can examine out these design templates for yourself on the HostGator website without having to sign up.
Free website home builders.
With an account, you can quickly develop an internet site with one of two website builders you get access to. The 2 website contractors are:.
Trendy Site Builder, and.
Website Studio website contractor.
Note, you can just use the website contractors for one website on your account. Exactly what this means is if you get an account where you can host unrestricted domains, you can just construct one website with a website contractor.
Email accounts.
You get endless POP3 e-mail accounts with SMTP. Having e-mail accounts on your customized domain names is more professional than a gmail or hotmail e-mail account.
45 day cash back assure.
You can get your refund if you cancel your account within 45 days if HostGator isn't for you.
Video tutorials.
HostGator offers you access to many video tutorials that step you with many processes.
Consumer support.
You can access live consumer support by means of the telephone and live talk. The operators for technical support know a lot about working in HostGator. Note, nonetheless, you will not get much help with specific scripts such as WordPress. If you have a concern about tailoring a WordPress theme, HostGator won't help you (I found this to be the case with Bluehost. What I do in these scenarios is inquire on my premium WordPress style support online forum and/or do general Google searches).
1 Criticism of HostGator.
I needed to call HostGator to verify my account upon opening it. This didn't take long, but it was an extra action. I would have chosen just to sign up and get going without having to call them for confirmation.
The Miller theorem refers to the process of creating equivalent circuits. It asserts that a floating impedance element, supplied by two voltage sources connected in series, may be split into two grounded elements with corresponding impedances. There is also a dual Miller theorem with regards to impedance supplied by two current sources connected in parallel. The two versions are based on the two Kirchhoff's circuit laws.
Miller theorems are not only pure mathematical expressions. These arrangements explain important circuit phenomena about modifying impedance (Miller effect, virtual ground, bootstrapping, negative impedance, etc.) and help in designing and understanding various commonplace circuits (feedback amplifiers, resistive and time-dependent converters, negative impedance converters, etc.). The theorems are useful in 'circuit analysis' especially for analyzing circuits with feedback[1] and certain transistor amplifiers at high frequencies.[2]
There is a close relationship between Miller theorem and Miller effect: the theorem may be considered as a generalization of the effect and the effect may be thought as of a special case of the theorem.
Miller theorem (for voltages)
Definition
The Miller theorem establishes that in a linear circuit, if there exists a branch with impedance Z, connecting two nodes with nodal voltages V1 and V2, we can replace this branch by two branches connecting the corresponding nodes to ground by impedances respectively Z/(1 − K) and KZ/(K − 1), where K = V2/V1. The Miller theorem may be proved by using the equivalent two-port network technique to replace the two-port to its equivalent and by applying the source absorption theorem.[3] This version of the Miller theorem is based on Kirchhoff's voltage law; for that reason, it is named also Miller theorem for voltages.
Explanation
Miller theorem implies that an impedance element is supplied by two arbitrary (not necessarily dependent) voltage sources that are connected in series through the common ground. In practice, one of them acts as a main (independent) voltage source with voltage V1 and the other – as an additional (linearly dependent) voltage source with voltage . The idea of Miller theorem (modifying circuit impedances seen from the sides of the input and output sources) is revealed below by comparing the two situations – without and with connecting an additional voltage source V2.
If V2 was zero (there was not a second voltage source or the right end of the element with impedance Z was just grounded), the input current flowing through the element would be determined, according to Ohm's law, only by V1
and the input impedance of the circuit would be
As a second voltage source is included, the input current depends on both the voltages. According to its polarity, V2 is subtracted from or added to V1; so, the input current decreases/increases
and the input impedance of the circuit seen from the side of the input source accordingly increases/decreases
So, Miller theorem expresses the fact that connecting a second voltage source with proportional voltage in series with the input voltage source changes the effective voltage, the current and respectively, the circuit impedance seen from the side of the input source. Depending on the polarity, V2 acts as a supplemental voltage source helping or opposing the main voltage source to pass the current through the impedance.
Besides by presenting the combination of the two voltage sources as a new composed voltage source, the theorem may be explained by combining the actual element and the second voltage source into a new virtual element with dynamically modified impedance. From this viewpoint, V2 is an additional voltage that artificially increases/decreases the voltage drop Vz across the impedance Z thus decreasing/increasing the current. The proportion between the voltages determines the value of the obtained impedance (see the tables below) and gives in total six groups of typical applications.
The circuit impedance, seen from the side of the output source, may be defined similarly, if the voltages V1 and V2 are swapped and the coefficient K is replaced by 1/K
Implementation

Most frequently, the Miller theorem may be observed in, and implemented by, an arrangement consisting of an element with impedance Z connected between the two terminals of a grounded general linear network.[2] Usually, a voltage amplifier with gain of serves as such a linear network, but also other devices can play this role: a man and a potentiometer in a potentiometric null-balance meter, an electromechanical integrator (servomechanisms using potentiometric feedback sensors), etc.
In the amplifier implementation, the input voltage Vi serves as V1 and the output voltage Vo – as V2. In many cases, the input voltage source has some internal impedance or an additional input impedance is connected that, in combination with Z, introduces a feedback. Depending on the kind of amplifier (non-inverting, inverting or differential), the feedback can be positive, negative or mixed.
The Miller amplifier arrangement has two aspects:
- the amplifier may be thought as an additional voltage source converting the actual impedance into a virtual impedance (the amplifier modifies the impedance of the actual element)
- the virtual impedance may be thought as an element connected in parallel to the amplifier input (the virtual impedance modifies the amplifier input impedance).
Applications
The introduction of an impedance that connects amplifier input and output ports adds a great deal of complexity in the analysis process. Miller theorem helps reduce the complexity in some circuits particularly with feedback[2] by converting them to simpler equivalent circuits. But Miller theorem is not only an effective tool for creating equivalent circuits; it is also a powerful tool for designing and understanding circuits based on modifying impedance by additional voltage. Depending on the polarity of the output voltage versus the input voltage and the proportion between their magnitudes, there are six groups of typical situations. In some of them, the Miller phenomenon appears as desired (bootstrapping) or undesired (Miller effect) unintentional effects; in other cases it is intentionally introduced.
Applications based on subtracting V2 from V1
In these applications, the output voltage Vo is inserted with an opposite polarity in respect to the input voltage Vi travelling along the loop (but in respect to ground, the polarities are the same). As a result, the effective voltage across, and the current through, the impedance decrease; the input impedance increases.
<increased>...</increased>Increased impedance is implemented by a non-inverting amplifier with gain of 0 < Av < 1. The (magnitude of) output voltage is less than the input voltage Vi and partially neutralizes it. Examples are imperfect voltage followers (emitter, source, cathode follower, etc.) and amplifiers with series negative feedback (emitter degeneration), whose input impedance is moderately increased.
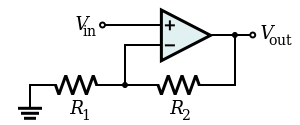
<infinite>...</infinite>Infinite impedance uses a non-inverting amplifier with Av = 1. The output voltage is equal to the input voltage Vi and completely neutralizes it. Examples are potentiometric null-balance meters and op-amp followers and amplifiers with series negative feedback (op-amp follower and non-inverting amplifier) where the circuit input impedance is enormously increased. This technique is referred to as bootstrapping and is intentionally used in biasing circuits, input guarding circuits,[4] etc.
<negative current inversion>...</negative current inversion>Negative impedance obtained by current inversion is implemented by a non-inverting amplifier with Av > 1. The current changes its direction, as the output voltage is higher than the input voltage. If the input voltage source has some internal impedance or if it is connected through another impedance element, a positive feedback appears. A typical application is the negative impedance converter with current inversion (INIC) that uses both negative and positive feedback (the negative feedback is used to realize a non-inverting amplifier and the positive feedback – to modify the impedance).
Applications based on adding V2 to V1
In these applications, the output voltage Vo is inserted with the same polarity in respect to the input voltage Vi travelling along the loop (but in respect to ground, the polarities are opposite). As a result, the effective voltage across and the current through the impedance increase; the input impedance decreases.
<decreased>...</decreased>Decreased impedance is implemented by an inverting amplifier having some moderate gain, usually 10 < Av < 1000. It may be observed as an undesired Miller effect in common-emitter, common-source and common-cathode amplifying stages where effective input capacitance is increased. Frequency compensation for general purpose operational amplifiers and transistor Miller integrator are examples of useful usage of the Miller effect.
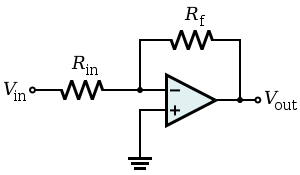
<zeroed>...</zeroed>Zeroed impedance uses an inverting (usually op-amp) amplifier with enormously high gain Av → ∞. The output voltage is almost equal to the voltage drop VZ across the impedance and completely neutralizes it. The circuit behaves as a short connection and a virtual ground appears at the input; so, it should not be driven by a constant voltage source. For this purpose, some circuits are driven by a constant current source or by a real voltage source with internal impedance: current-to-voltage converter (transimpedance amplifier), capacitive integrator (named also current integrator or charge amplifier), resistance-to-voltage converter (a resistive sensor connected in the place of the impedance Z).
The rest of them have additional impedance connected in series to the input: voltage-to-current converter (transconductance amplifier), inverting amplifier, summing amplifier, inductive integrator, capacitive differentiator, resistive-capacitive integrator, capacitive-resistive differentiator, inductive-resistive differentiator, etc. The inverting integrators from this list are examples of useful and desired applications of the Miller effect in its extreme manifestation.
In all these op-amp inverting circuits with parallel negative feedback, the input current is increased to its maximum. It is determined only by the input voltage and the input impedance according to Ohm's law; it does not depend on the impedance Z.
<negative with voltage inversion>...</negative with voltage inversion>Negative impedance with voltage inversion is implemented by applying both negative and positive feedback to an op-amp amplifier with a differential input. The input voltage source has to have internal impedance > 0 or it has to be connected through another impedance element to the input. Under these conditions, the input voltage Vi of the circuit changes its polarity as the output voltage exceeds the voltage drop VZ across the impedance (Vi = Vz – Vo < 0).
A typical application is a negative impedance converter with voltage inversion (VNIC).[5] It is interesting that the circuit input voltage has the same polarity as the output voltage, although it is applied to the inverting op-amp input; the input source has an opposite polarity to both the circuit input and output voltages.
Generalization of Miller arrangement
The original Miller effect is implemented by capacitive impedance connected between the two nodes. Miller theorem generalizes Miller effect as it implies arbitrary impedance Z connected between the nodes. It is supposed also a constant coefficient K; then the expressions above are valid. But modifying properties of Miller theorem exist even when these requirements are violated and this arrangement can be generalized further by dynamizing the impedance and the coefficient.
Non-linear element. Besides impedance, Miller arrangement can modify the IV characteristic of an arbitrary element. The circuit of a diode log converter is an example of a non-linear virtually zeroed resistance where the logarithmic forward IV curve of a diode is transformed to a vertical straight line overlapping the Y axis.
Not constant coefficient. If the coefficient K varies, some exotic virtual elements can be obtained. A gyrator circuit is an example of such a virtual element where the resistance RL is modified so that to mimic inductance, capacitance or inversed resistance.
Dual Miller theorem (for currents)
Definition
There is also a dual version of Miller theorem that is based on Kirchhoff's current law (Miller theorem for currents): if there is a branch in a circuit with impedance Z connecting a node, where two currents I1 and I2 converge to ground, we can replace this branch by two conducting the referred currents, with impedances respectively equal to (1 + α)Z and (1 + α)Z/α, where α = I2/I1. The dual theorem may be proved by replacing the two-port network by its equivalent and by applying the source absorption theorem.[3]
Explanation
Dual Miller theorem actually expresses the fact that connecting a second current source producing proportional current in parallel with the main input source and the impedance element changes the current flowing through it, the voltage and accordingly, the circuit impedance seen from the side of the input source. Depending on the direction, I2 acts as a supplemental current source helping or opposing the main current source I1 to create voltage across the impedance. The combination of the actual element and the second current source may be thought as of a new virtual element with dynamically modified impedance.
Implementation
Dual Miller theorem is usually implemented by an arrangement consisting of two voltage sources supplying the grounded impedance Z through floating impedances (see Fig. 3). The combinations of the voltage sources and belonging impedances form the two current sources – the main and the auxiliary one. As in the case of the main Miller theorem, the second voltage is usually produced by a voltage amplifier. Depending on the kind of the amplifier (inverting, non-inverting or differential) and the gain, the circuit input impedance may be virtually increased, infinite, decreased, zero or negative.
Applications
As the main Miller theorem, besides helping circuit analysis process, the dual version is a powerful tool for designing and understanding circuits based on modifying impedance by additional current. Typical applications are some exotic circuits with negative impedance as load cancellers,[6] capacitance neutralizers,[7] Howland current source and its derivative Deboo integrator.[8] In the last example (see Fig. 1 there), the Howland current source consists of an input voltage source VIN, a positive resistor R, a load (the capacitor C acting as impedance Z) and a negative impedance converter INIC (R1 = R2 = R3 = R and the op-amp). The input voltage source and the resistor R constitute an imperfect current source passing current IR through the load (see Fig. 3 in the source). The INIC acts as a second current source passing "helping" current I-R through the load. As a result, the total current flowing through the load is constant and the circuit impedance seen by the input source is increased. As a comparison, in a load canceller, the INIC passes all the required current through the load; the circuit impedance seen from the side of the input source (the load impedance) is almost infinite.
List of specific applications based on Miller theorems
Below is a list of circuit solutions, phenomena and techniques based on the two Miller theorems.
- Potentiometric null-balance meter
- Electromechanical data recorders with a potentiometric servo system
- Emitter (source, cathode) follower
- Transistor amplifier with emitter (source, cathode) degeneration
- Transistor bootstrapped biasing circuits
- Transistor integrator
- Common-emitter (common-source, common-cathode) amplifying stages with stray capacitances
- Op-amp follower
- Op-amp non-inverting amplifier
- Op-amp bootstrapped AC follower with high input impedance
- Bilateral current source
- Negative impedance converter with current inversion (INIC)
- Negative impedance load canceller
- Negative impedance input capacitance canceller
- Howland current source
- Deboo integrator
- Op-amp inverting ammeter
- Op-amp voltage-to-current converter (transconductance amplifier)
- Op-amp current-to-voltage converter (transimpedance amplifier)
- Op-amp resistance-to-current converter
- Op-amp resistance-to-voltage converter
- Op-amp inverting amplifier
- Op-amp inverting summer
- Op-amp inverting capacitive integrator (current integrator, charge amplifier)
- Op-amp inverting resistive-capacitive integrator
- Op-amp inverting capacitive differentiator
- Op-amp inverting capacitive-resistive differentiator
- Op-amp inverting inductive integrator
- Op-amp inverting inductive-resistive differentiator, etc.
- Op-amp diode log converter
- Op-amp diode anti-log converter
- Op-amp inverting diode limiter (precision diode)
- Negative impedance converter with voltage inversion (VNIC), etc.
- Bootstrapping
- Input guarding of high impedance op-amp circuits
- Input-capacitance neutralization
- Virtual ground
- Miller effect
- Frequency op-amp compensation
- Negative impedance
- Load cancelling
See also
References
- ↑ Template:Cite web
- ↑ 2.0 2.1 2.2 Template:Cite web
- ↑ 3.0 3.1 Template:Cite web
- ↑ Working with High Impedance Op Amps AN-241
- ↑ Template:Cite web
- ↑ Negative-resistance load canceller helps drive heavy loads
- ↑ Impedance and admittance transformations using operational amplifiers by D. H. Sheingold
- ↑ Template:Cite web
External links
- Miller's theorem revisited
- New Results Related to Miller’s Theorem
- A network theorem dual to Miller's theorem
- Generalized Miller theorem and its applications
- The Feedback Decomposition Theorem (FDT): The evolution of Miller's Theorem
- An Accurate Calculation of Miller Effect on the Frequency Response and on the Input and Output Impedances of Feedback Amplifiers (using FDT)
Further reading
- Fundamentals of Microelectronics by Behzad Razavi
- Microelectronic Circuits by Adel Sedra and Kenneth Smith
- Fundamentals of RF Circuit Design by Jeremy Everard








