Local consistency

In spherical trigonometry, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, analogous to the ordinary law of cosines from plane trigonometry.

Spherical triangle solved by the law of cosines.

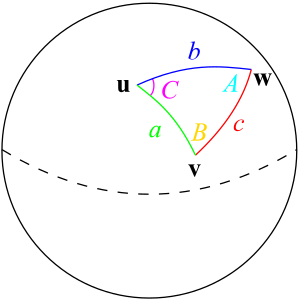
Given a unit sphere, a "spherical triangle" on the surface of the sphere is defined by the great circles connecting three points u, v, and w on the sphere (shown at right). If the lengths of these three sides are a (from u to v), b (from u to w), and c (from v to w), and the angle of the corner opposite c is C, then the (first) spherical law of cosines states:

$\cos (c)=\cos (a)\cos (b)+\sin (a)\sin (b)\cos (C).$

Since this is a unit sphere, the lengths a, b, and c are simply equal to the angles (in radians) subtended by those sides from the center of the sphere (for a non-unit sphere, they are the distances divided by the radius). As a special case, for $C=\pi /2$, then $\cos (C)=0$ and one obtains the spherical analogue of the Pythagorean theorem:

$\cos (c)=\cos (a)\cos (b).$

A variation on the law of cosines, the second spherical law of cosines, (also called the cosine rule for angles) states:

$\cos (A)=-\cos (B)\cos (C)+\sin (B)\sin (C)\cos (a)$

where A and B are the angles of the corners opposite to sides a and b, respectively. It can be obtained from consideration of a spherical triangle dual to the given one.

If the law of cosines is used to solve for c, the necessity of inverting the cosine magnifies rounding errors when c is small. In this case, the alternative formulation of the law of haversines is preferable.

Proof

A proof of the law of cosines can be constructed as follows. Let u, v, and w denote the unit vectors from the center of the sphere to those corners of the triangle. Then, the lengths (angles) of the sides are given by the dot products:

$\cos (a)=\mathbf{u}\cdot \mathbf{v}$

$\cos (b)=\mathbf{u}\cdot \mathbf{w}$

$\cos (c)=\mathbf{v}\cdot \mathbf{w}$

To get the angle C, we need the tangent vectors t_a and t_b at u along the directions of sides a and b, respectively. For example, the tangent vector t_a is the unit vector perpendicular to u in the u-v plane, whose direction is given by the component of v perpendicular to u. This means:

${\mathbf{t}}_a=\frac{\mathbf{v}-\mathbf{u}(\mathbf{u}\cdot \mathbf{v})}{|\mathbf{v}-\mathbf{u}(\mathbf{u}\cdot \mathbf{v})|}=\frac{\mathbf{v}-\mathbf{u}\cos (a)}{\sin (a)}$

where for the denominator we have used the Pythagorean identity sin²(a) = 1 − cos²(a). Similarly,

${\mathbf{t}}_b=\frac{\mathbf{w}-\mathbf{u}\cos (b)}{\sin (b)}.$

Then, the angle C is given by:

$\cos (C)={\mathbf{t}}_a\cdot {\mathbf{t}}_b=\frac{\cos (c)-\cos (a)\cos (b)}{\sin (a)\sin (b)}$

from which the law of cosines immediately follows.

Proof without vectors

To the diagram above, add a plane tangent to the sphere at u, and extend radii from the center of the sphere O through v and through w to meet the plane at points y and z. We then have two plane triangles with a side in common: the triangle containing u, y and z and the one containing O, y and z. Sides of the first triangle are tan a and tan b, with angle C between them; sides of the second triangle are sec a and sec b, with angle c between them. By the law of cosines for plane triangles (and remembering that ${\sec }^2$ of any angle is ${\tan }^2+1$),

${\tan }^{2}a+{\tan }^{2}b-2\tan a\tan b\cos C={\sec }^{}a+{\sec }^{}b-2\sec a\sec b\cos c$

$=2+{\tan }^{2}a+{\tan }^{2}b-2\sec a\sec b\cos c$

So

$-\tan a\tan b\cos C=1-\sec a\sec b\cos c$

Multiply both sides by $\cos a\cos b$ and rearrange.

Planar limit: small angles

For small spherical triangles, i.e. for small a, b, and c, the spherical law of cosines is approximately the same as the ordinary planar law of cosines,

$c^2\approx a^2+b^2-2ab\cos (C).$

To prove this, we'll use the small-angle approximation obtained from the Maclaurin series for the cosine and sine functions:

$\cos (a)=1-\frac{a^2}{2}+O(a^4),\sin (a)=a+O(a^3)$

Substituting these expressions into the spherical law of cosines nets:

$1-\frac{c^2}{2}+O(c^4)=1-\frac{a^2}{2}-\frac{b^2}{2}+\frac{a^2{b}^2}{4}+O(a^4)+O(b^4)+\cos (C)(ab+O(a^{3}b)+O(a{b}^3)+O(a^3{b}^3))$

or after simplifying:

$c^2=a^2+b^2-2ab\cos (C)+O(c^4)+O(a^4)+O(b^4)+O(a^2{b}^2)+O(a^{3}b)+O(a{b}^3)+O(a^3{b}^3).$

Remembering the properties of big O notation, we can discard summands where the lowest exponent for a or b is greater than 1, so finally, the error in this approximation is:

$O(c^4)+O(a^{3}b)+O(a{b}^3).$

See also

• Half-side formula
• Hyperbolic law of cosines
• Solution of triangles