Narumi polynomials

In geometry, a pentagonal polytope is a regular polytope in n dimensions constructed from the H_n Coxeter group. The family was named by George Olshevsky, because the two-dimensional pentagonal polytope is a pentagon. It can be named by its Schläfli symbol as {5, 3^{n − 1}} (dodecahedral) or {3^{n − 1}, 5} (icosahedral).

Family members

The family starts as 1-polytopes and ends with n = 5 as infinite tessellations of 4-dimensional hyperbolic space.

There are two types of pentagonal polytopes; they may be termed the dodecahedral and icosahedral types, by their three-dimensional members. The two types are duals of each other.

Dodecahedral

The complete family of dodecahedral pentagonal polytopes are:

1. Line segment, { }
2. Pentagon, {5}
3. Dodecahedron, {5, 3} (12 pentagonal faces)
4. 120-cell, {5, 3, 3} (120 dodecahedral cells)
5. Order-3 120-cell honeycomb, {5, 3, 3, 3} (tessellates hyperbolic 4-space (∞ 120-cell facets)

The facets of each dodecahedral pentagonal polytope are the dodecahedral pentagonal polytopes of one less dimension. Their vertex figures are the simplices of one less dimension.

Dodecahedral pentagonal polytopes

n	Coxeter group	Petrie polygon projection	Name Coxeter-Dynkin diagram Schläfli symbol	Facets	Elements
					Vertices	Edges	Faces	Cells	4-faces
1	$H_1$		Line segment Template:CDD { }	2 vertices	2
2	$H_2$		Pentagon Template:CDD {5}	5 edges	5	5
3	$H_3$		Dodecahedron Template:CDD {5, 3}	12 pentagons	20	30	12
4	$H_4$		120-cell Template:CDD {5, 3, 3}	120 dodecahedra	600	1200	720	120
5	${\overline{H}}_4$		Order-3 120-cell honeycomb Template:CDD {5, 3, 3, 3}	∞ 120-cells	∞	∞	∞	∞	∞

Icosahedral

The complete family of icosahedral pentagonal polytopes are:

1. Line segment, { }
2. Pentagon, {5}
3. Icosahedron, {3, 5} (20 triangular faces)
4. 600-cell, {3, 3, 5} (120 tetrahedron cells)
5. Order-5 5-cell honeycomb, {3, 3, 3, 5} (tessellates hyperbolic 4-space (∞ 5-cell facets)

The facets of each icosahedral pentagonal polytope are the simplices of one less dimension. Their vertex figures are icosahedral pentagonal polytopes of one less dimension.

Icosahedral pentagonal polytopes

n	Coxeter group	Petrie polygon projection	Name Coxeter-Dynkin diagram Schläfli symbol	Facets	Elements
					Vertices	Edges	Faces	Cells	4-faces
1	$H_1$		Line segment Template:CDD { }	2 vertices	2
2	$H_2$		Pentagon Template:CDD {5}	5 Edges	5	5
3	$H_3$		Icosahedron Template:CDD {3, 5}	20 equilateral triangles	12	30	20
4	$H_4$		600-cell Template:CDD {3, 3, 5}	600 tetrahedra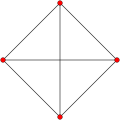	120	720	1200	600
5	${\overline{H}}_4$		Order-5 5-cell honeycomb Template:CDD {3, 3, 3, 5}	∞ 5-cells	∞	∞	∞	∞	∞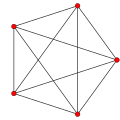

Related star polytopes and honeycombs

The pentagonal polytopes can be stellated to form new star regular polytopes. In two dimensions, this forms the pentagram {⁵/₂}; in three dimensions, this forms the four Kepler–Poinsot polyhedra, {3, ⁵/₂}, {⁵/₂, 3}, {5, ⁵/₂}, and {⁵/₂, 5}; and in four dimensions, this forms the ten Schläfli–Hess polychora: {3, 5, ⁵/₂}, {⁵/₂, 5, 3}, {5, ⁵/₂, 5}, {5, 3, ⁵/₂}, {⁵/₂, 3, 5}, {⁵/₂, 5, ⁵/₂}, {5, ⁵/₂, 3}, {3, ⁵/₂, 5}, {3, 3, ⁵/₂}, and {⁵/₂, 3, 3}. In four-dimensional hyperbolic space there are four regular star-honeycombs: {⁵/₂, 5, 3, 3}, {3, 3, 5, ⁵/₂}, {3, 5, ⁵/₂, 5}, and {5, ⁵/₂, 5, 3}.

Notes

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

References

• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 10) H.S.M. Coxeter, Star Polytopes and the Schlafli Function f(α,β,γ) [Elemente der Mathematik 44 (2) (1989) 25–36]
• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Table I(ii): 16 regular polytopes {p, q,r} in four dimensions, pp. 292–293)