Butterfly curve (algebraic): Difference between revisions
en>Giftlite m +. |
en>Mark viking added wl |
||
| Line 1: | Line 1: | ||
The '''torsion constant''' is a geometrical property of a bar's cross-section which is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear-elastic bar. The torsion constant, together with material properties and length, describes a bar's torsional [[stiffness]]. The SI unit for torsion constant is m<sup>4</sup>. | |||
== History == | |||
In 1820, the French engineer A. Duleau derived analytically that the torsion constant of a beam is identical to the [[second moment of area]] normal to the section J<sub>zz</sub>, which has an exact analytic equation, by assuming that a plane section before twisting remains plane after twisting, and a diameter remains a straight line. | |||
Unfortunately, that assumption is correct only in beams with circular cross-sections, and is incorrect for any other shape.<ref> | |||
Archie Higdon et al. | |||
"Mechanics of Materials, 4th edition". | |||
</ref> | |||
For non-circular cross-sections, there are no exact analytical equations for finding the torsion constant. However approximate solutions have been found for many shapes. | |||
Non-circular cross-section always have warping deformations that require numerical methods to allow the exact calculation of the torsion constant.<ref name="David">Advanced structural mechanics, 2nd Edition, David Johnson</ref> | |||
== Partial Derivation == | |||
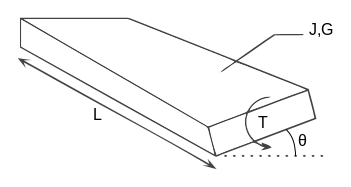
For a beam of uniform cross-section along its length: | |||
:<math>\theta = \frac{TL}{JG}</math> | |||
where | |||
:<math>\theta</math> is the angle of twist in radians | |||
:''T'' is the applied torque | |||
:''L'' is the beam length | |||
:''J'' is the torsion constant | |||
:''G'' is the [[Modulus of rigidity]] (shear modulus) of the material | |||
[[File:TorsionConstantBar.svg]] | |||
==Examples for specific uniform cross-sectional shapes== | |||
===Circle=== | |||
:<math>J_{zz} = J_{xx}+J_{yy} = \frac{\pi r^4}{4} + \frac{\pi r^4}{4} = \frac{\pi r^4}{2}</math><ref name="Weisstein, Eric W.">"Area Moment of Inertia." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/AreaMomentofInertia.html</ref> | |||
where | |||
:''r'' is the radius | |||
This is identical to the [[second moment of area]] J<sub>zz</sub> and is exact. | |||
alternatively write: <math>J = \frac{\pi D^4}{32}</math><ref name="Weisstein, Eric W.">"Area Moment of Inertia." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/AreaMomentofInertia.html</ref> | |||
where | |||
:''D'' is the Diameter | |||
===Ellipse=== | |||
:<math>J \approx \frac{\pi a^3 b^3}{a^2 + b^2}</math><ref name="Roark7">Roark's Formulas for stress & Strain, 7th Edition, Warren C. Young & Richard G. Budynas</ref><ref name="Irjens">Continuum Mechanics, Fridtjov Irjens, Springer 2008, p238, ISBN 978-3-540-74297-5</ref> | |||
where | |||
:''a'' is the major radius | |||
:''b'' is the minor radius | |||
===Square=== | |||
:<math>J \approx \,2.25 a^4</math><ref name="RoyMech7">Torsion Equations, Roy Beardmore, http://www.roymech.co.uk/Useful_Tables/Torsion/Torsion.html</ref> | |||
where | |||
:''a'' is half the side length | |||
===Rectangle=== | |||
:<math>J \approx\beta a b^3</math> | |||
where | |||
:''a'' is the length of the long side | |||
:''b'' is the length of the short side | |||
:<math>\beta</math> is found from the following table: | |||
{| class="wikitable" | |||
|- | |||
! a/b | |||
! <math>\beta</math> | |||
|- | |||
| 1.0 | |||
| 0.141 | |||
|- | |||
| 1.5 | |||
| 0.196 | |||
|- | |||
| 2.0 | |||
| 0.229 | |||
|- | |||
| 2.5 | |||
| 0.249 | |||
|- | |||
| 3.0 | |||
| 0.263 | |||
|- | |||
| 4.0 | |||
| 0.281 | |||
|- | |||
| 5.0 | |||
| 0.291 | |||
|- | |||
| 6.0 | |||
| 0.299 | |||
|- | |||
| 10.0 | |||
| 0.312 | |||
|- | |||
| <math>\infty</math> | |||
| 0.333 | |||
|}<ref>Advanced Strength and Applied Elasticity, Ugural & Fenster, Elsevier, ISBN 0-444-00160-3</ref> | |||
Alternatively the following equation can be used with an error of not greater than 4%:<br> | |||
:<math>J \approx a b^3 \left ( \frac{1}{3}-0.21 \frac{b}{a} \left ( 1- \frac{b^4}{12a^4} \right ) \right )</math><ref name="Roark7" /> | |||
===Thin walled closed tube of uniform thickness=== | |||
:<math>J = \frac{4A^2t}{U}</math><ref name="Roark">Roark's Formulas for stress & Strain, 6th Edition, Warren C. Young</ref> | |||
:''A'' is the mean of the areas enclosed by the inner and outer boundaries | |||
:''t'' is the wall thickness | |||
:''U'' is the length of the median boundary | |||
===Thin walled open tube of uniform thickness=== | |||
:<math>J = \frac{1}{3}U t^3</math><ref>Advanced Mechanics of Materials, Boresi, John Wiley & Sons, ISBN 0-471-55157-0</ref> | |||
:''t'' is the wall thickness | |||
:''U'' is the length of the median boundary (perimeter of median cross section) | |||
===Circular thin walled open tube of uniform thickness (approximation)=== | |||
This is a tube with a slit cut longitudinally through its wall. | |||
:<math>J = \frac{2}{3} \pi r t^3</math><ref name="Roark" /> | |||
:''t'' is the wall thickness | |||
:''r'' is the mean radius | |||
This is derived from the above equation for an arbitrary thin walled open tube of uniform thickness. | |||
==Commercial Products == | |||
There are a number specialized software tools to calculate the torsion constant using the finite element method. | |||
* [http://www.mechatools.com/en/shapedesigner.html ShapeDesigner] by [http://www.mechatools.com Mechatools Technologies] | |||
* [http://www.iesweb.com/products/shapebuilder/index.htm ShapeBuilder] by [http://www.iesweb.com IES Web] | |||
* [http://www.bentley.com/en-US/Products/STAAD.Pro/Section-wizard.htm STAAD SectionWizard] by [http://www.bentley.com Bentley] | |||
* [http://fornamagic.com/download.php?view.15 SectionAnalyzer] by [http://www.fornamagic.com Fornamagic Ltd] | |||
* [http://strand7.com Strand7 BXS Generator] by [http://www.strand7.com Strand7 Pty Limited] | |||
==References== | |||
{{reflist}} | |||
{{DEFAULTSORT:Torsion Constant}} | |||
[[Category:Continuum mechanics]] | |||
[[Category:Structural analysis]] | |||
Revision as of 00:12, 25 July 2013
The torsion constant is a geometrical property of a bar's cross-section which is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear-elastic bar. The torsion constant, together with material properties and length, describes a bar's torsional stiffness. The SI unit for torsion constant is m4.
History
In 1820, the French engineer A. Duleau derived analytically that the torsion constant of a beam is identical to the second moment of area normal to the section Jzz, which has an exact analytic equation, by assuming that a plane section before twisting remains plane after twisting, and a diameter remains a straight line. Unfortunately, that assumption is correct only in beams with circular cross-sections, and is incorrect for any other shape.[1]
For non-circular cross-sections, there are no exact analytical equations for finding the torsion constant. However approximate solutions have been found for many shapes. Non-circular cross-section always have warping deformations that require numerical methods to allow the exact calculation of the torsion constant.[2]
Partial Derivation
For a beam of uniform cross-section along its length:
where
- is the angle of twist in radians
- T is the applied torque
- L is the beam length
- J is the torsion constant
- G is the Modulus of rigidity (shear modulus) of the material
Examples for specific uniform cross-sectional shapes
Circle
where
- r is the radius
This is identical to the second moment of area Jzz and is exact.
alternatively write: [3] where
- D is the Diameter
Ellipse
where
- a is the major radius
- b is the minor radius
Square
where
- a is half the side length
Rectangle
where
- a is the length of the long side
- b is the length of the short side
- is found from the following table:
| a/b | |
|---|---|
| 1.0 | 0.141 |
| 1.5 | 0.196 |
| 2.0 | 0.229 |
| 2.5 | 0.249 |
| 3.0 | 0.263 |
| 4.0 | 0.281 |
| 5.0 | 0.291 |
| 6.0 | 0.299 |
| 10.0 | 0.312 |
| 0.333 |
Alternatively the following equation can be used with an error of not greater than 4%:
Thin walled closed tube of uniform thickness
- [8]
- A is the mean of the areas enclosed by the inner and outer boundaries
- t is the wall thickness
- U is the length of the median boundary
Thin walled open tube of uniform thickness
- [9]
- t is the wall thickness
- U is the length of the median boundary (perimeter of median cross section)
Circular thin walled open tube of uniform thickness (approximation)
This is a tube with a slit cut longitudinally through its wall.
- [8]
- t is the wall thickness
- r is the mean radius
This is derived from the above equation for an arbitrary thin walled open tube of uniform thickness.
Commercial Products
There are a number specialized software tools to calculate the torsion constant using the finite element method.
- ShapeDesigner by Mechatools Technologies
- ShapeBuilder by IES Web
- STAAD SectionWizard by Bentley
- SectionAnalyzer by Fornamagic Ltd
- Strand7 BXS Generator by Strand7 Pty Limited
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- ↑ Archie Higdon et al. "Mechanics of Materials, 4th edition".
- ↑ Advanced structural mechanics, 2nd Edition, David Johnson
- ↑ 3.0 3.1 "Area Moment of Inertia." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/AreaMomentofInertia.html
- ↑ 4.0 4.1 Roark's Formulas for stress & Strain, 7th Edition, Warren C. Young & Richard G. Budynas
- ↑ Continuum Mechanics, Fridtjov Irjens, Springer 2008, p238, ISBN 978-3-540-74297-5
- ↑ Torsion Equations, Roy Beardmore, http://www.roymech.co.uk/Useful_Tables/Torsion/Torsion.html
- ↑ Advanced Strength and Applied Elasticity, Ugural & Fenster, Elsevier, ISBN 0-444-00160-3
- ↑ 8.0 8.1 Roark's Formulas for stress & Strain, 6th Edition, Warren C. Young
- ↑ Advanced Mechanics of Materials, Boresi, John Wiley & Sons, ISBN 0-471-55157-0