Exponential decay

In mathematics, a monoidal category (or tensor category) is a category C equipped with a bifunctor

⊗ : C × C → C

which is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism. The associated natural isomorphisms are subject to certain coherence conditions which ensure that all the relevant diagrams commute. In a monoidal category, analogs of usual monoids from abstract algebra can be defined using the same commutative diagrams. In fact, usual monoids are exactly the monoid objects in the monoidal category of sets with Cartesian product.

The ordinary tensor product makes vector spaces, abelian groups, R-modules, or R-algebras into monoidal categories. Monoidal categories can be seen as a generalization of these and other examples.

In category theory, monoidal categories can be used to define the concept of a monoid object and an associated action on the objects of the category. They are also used in the definition of an enriched category.

Monoidal categories have numerous applications outside of category theory proper. They are used to define models for the multiplicative fragment of intuitionistic linear logic. They also form the mathematical foundation for the topological order in condensed matter. Braided monoidal categories have applications in quantum field theory and string theory.

Formal definition

A monoidal category is a category $\mathbf {C}$ equipped with

• a bifunctor $\otimes \colon \mathbf {C} \times \mathbf {C} \to \mathbf {C}$ called the tensor product or monoidal product,
• an object $I$ called the unit object or identity object,
• three natural isomorphisms subject to certain coherence conditions expressing the fact that the tensor operation
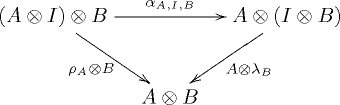
  • is associative: there is a natural isomorphism $\alpha$, called associator, with components $\alpha _{A,B,C}\colon (A\otimes B)\otimes C\cong A\otimes (B\otimes C)$,
  • has $I$ as left and right identity: there are two natural isomorphisms $\lambda$ and $\rho$, respectively called left and right unitor, with components $\lambda _{A}\colon I\otimes A\cong A$ and $\rho _{A}\colon A\otimes I\cong A$.

The coherence conditions for these natural transformations are:

• for all $A$, $B$, $C$ and $D$ in $\mathbf {C}$, the pentagon diagram

commutes;

• for all $A$ and $B$ in $\mathbf {C}$, the triangle diagram

commutes;

It follows from these three conditions that a large class of such diagrams (i.e. diagrams whose morphisms are built using $\alpha$, $\lambda$, $\rho$, identities and tensor product) commute: this is Mac Lane's "coherence theorem". It is sometimes inaccurately stated that all such diagrams commute.

A strict monoidal category is one for which the natural isomorphisms α, λ and ρ are identities. Every monoidal category is monoidally equivalent to a strict monoidal category.

Examples

• Any category with finite products is monoidal with the product as the monoidal product and the terminal object as the unit. Such a category is sometimes called a cartesian monoidal category. For example:
  • Set, the category of sets with the Cartesian product, one-element sets serving as the unit.
• Any category with finite coproducts is monoidal with the coproduct as the monoidal product and the initial object as the unit.
• R-Mod, the category of modules over a commutative ring R, is a monoidal category with the tensor product of modules ⊗_R serving as the monoidal product and the ring R (thought of as a module over itself) serving as the unit. As special cases one has:
  • K-Vect, the category of vector spaces over a field K, with the one-dimensional vector space K serving as the unit.
  • Ab, the category of abelian groups, with the group of integers Z serving as the unit.
• For any commutative ring R, the category of R-algebras is monoidal with the tensor product of algebras as the product and R as the unit.
• The category of pointed spaces is monoidal with the smash product serving as the product and the pointed 0-sphere (a two-point discrete space) serving as the unit.
• The category of all endofunctors on a category C is a strict monoidal category with the composition of functors as the product and the identity functor as the unit.
• Just like for any category E, the full subcategory spanned by any given object is a monoid, it is the case that for any 2-category E, and any object C∈Ob(E), the full 2-subcategory of E spanned by {C} is a monoidal category. In the case E=Cat, we get the endofunctors example above.
• Bounded-above meet semilattices are strict symmetric monoidal categories: the product is meet and the identity is the top element.

Free strict monoidal category

For every category C, the free strict monoidal category Σ(C) can be constructed as follows:

• its objects are lists (finite sequences) A₁, ..., A_n of objects of C;
• there are arrows between two objects A₁, ..., A_m and B₁, ..., B_n only if m = n, and then the arrows are lists (finite sequences) of arrows f₁: A₁ → B₁, ..., f_n: A_n → B_n of C;
• the tensor product of two objects A₁, ..., A_n and B₁, ..., B_m is the concatenation A₁, ..., A_n, B₁, ..., B_m of the two lists, and, similarly, the tensor product of two morphisms is given by the concatenation of lists.

This operation Σ mapping category C to Σ(C) can be extended to a strict 2-monad on Cat.

See also

• Many monoidal categories have additional structure such as braiding, symmetry or closure: the references describe this in detail.
• Monoidal functors are the functors between monoidal categories which preserve the tensor product and monoidal natural transformations are the natural transformations, between those functors, which are "compatible" with the tensor product.
• There is a general notion of monoid object in a monoidal category, which generalizes the ordinary notion of monoid. In particular, a strict monoidal category can be seen as a monoid object in the category of categories Cat (equipped with the monoidal structure induced by the cartesian product).
• A monoidal category can also be seen as the category B(□, □) of a bicategory B with only one object, denoted □.
• Rigid categories are monoidal categories in which duals with nice properties exist.
• Autonomous categories (or compact closed categories) are monoidal categories in which inverses exist; they abstract the idea of FdVect, finite-dimensional vector spaces.
• Dagger symmetric monoidal categories, equipped with an extra dagger functor, abstracting the idea of FdHilb, finite-dimensional Hilbert spaces. These include the dagger compact categories.
• A category C enriched in a monoidal category M replaces the notion of a set of morphisms between pairs of objects in C with the notion of an M-object of morphisms between every two objects in C.
• Tannakian categories are monoidal categories enriched over a field which are very similar to representation categories of linear algebraic groups.
• Spherical category

References

• Joyal, André; Street, Ross (1993). "Braided Tensor Categories". Advances in Mathematics 102, 20–78.
• Kelly, G. Max (1964). "On MacLane's Conditions for Coherence of Natural Associativities, Commutativities, etc." Journal of Algebra 1, 397–402
• 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
  
  My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
• Mac Lane, Saunders (1963). "Natural Associativity and Commutativity". Rice University Studies 49, 28–46.
• Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd ed.). New York: Springer-Verlag.
• Template:Nlab

Sportspersons Hyslop from Nicolet, usually spends time with pastimes for example martial arts, property developers condominium in singapore singapore and hot rods. Maintains a trip site and has lots to write about after touring Gulf of Porto: Calanche of Piana.