Fermi's interaction

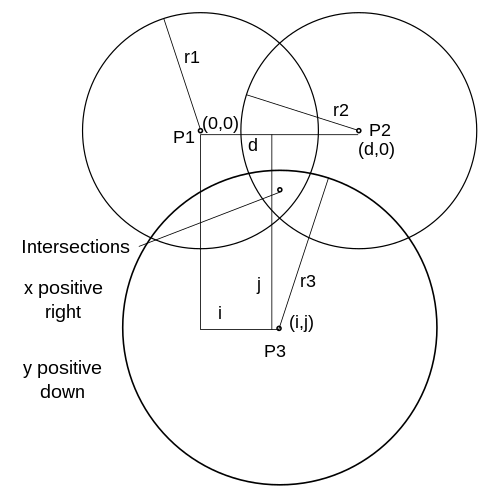
Figure 1. The plane z = 0, showing the three sphere centers, P1, P2, and P3; their x,y-coordinates; and the three sphere radii, r1, r2, and r3. The two intersections of the three sphere surfaces are directly in front and directly behind the point designated intersections in the z = 0 plane.

In geometry, trilateration is the process of determining absolute or relative locations of points by measurement of distances, using the geometry of circles, spheres or triangles. In addition to its interest as a geometric problem, trilateration does have practical applications in surveying and navigation, including global positioning systems (GPS). In contrast to triangulation, it does not involve the measurement of angles.

In two-dimensional geometry, it is known that if a point lies on two circles, then the circle centers and the two radii provide sufficient information to narrow the possible locations down to two. Additional information may narrow the possibilities down to one unique location.

In three-dimensional geometry, when it is known that a point lies on the surfaces of three spheres, then the centers of the three spheres along with their radii provide sufficient information to narrow the possible locations down to no more than two (unless the centers lie on a straight line).

This article describes a method for determining the intersections of three sphere surfaces given the centers and radii of the three spheres.

Derivation

The intersections of the surfaces of three spheres is found by formulating the equations for the three sphere surfaces and then solving the three equations for the three unknowns, x, y, and z. To simplify the calculations, the equations are formulated so that the centers of the spheres are on the z = 0 plane. Also, the formulation is such that one center is at the origin, and one other is on the x-axis. It is possible to formulate the equations in this manner since any three non-colinear points lie on a unique plane. After finding the solution, it can be transformed back to the original three dimensional Cartesian coordinate system.

We start with the equations for the three spheres:

$r_{1}^{2}=x^{2}+y^{2}+z^{2}\,$

$r_{2}^{2}=(x-d)^{2}+y^{2}+z^{2}\,$

$r_{3}^{2}=(x-i)^{2}+(y-j)^{2}+z^{2}\,$

We need to find a point located at (x, y, z) that satisfies all three equations.

First, we subtract the second equation from the first and solve for x:

$x={\frac {r_{1}^{2}-r_{2}^{2}+d^{2}}{2d}}.$

We assume that the first two spheres intersect in more than one point, that is that

$d-r_{1}<r_{2}<d+r_{1}.\,$

In this case, substituting the equation for x back into the equation for the first sphere produces the equation for a circle, the solution to the intersection of the first two spheres:

$y^{2}+z^{2}=r_{1}^{2}-{\frac {(r_{1}^{2}-r_{2}^{2}+d^{2})^{2}}{4d^{2}}}.$

Substituting $z^{2}=r_{1}^{2}-x^{2}-y^{2}$ into the formula for the third sphere and solving for y there results:

$y={\frac {r_{1}^{2}-r_{3}^{2}-x^{2}+(x-i)^{2}+j^{2}}{2j}}={\frac {r_{1}^{2}-r_{3}^{2}+i^{2}+j^{2}}{2j}}-{\frac {i}{j}}x.$

Now that we have the x- and y-coordinates of the solution point, we can simply rearrange the formula for the first sphere to find the z-coordinate:

$z=\pm {\sqrt {r_{1}^{2}-x^{2}-y^{2}}}.$

Now we have the solution to all three points x, y and z. Because z is expressed as the positive or negative square root, it is possible for there to be zero, one or two solutions to the problem.

This last part can be visualized as taking the circle found from intersecting the first and second sphere and intersecting that with the third sphere. If that circle falls entirely outside or inside of the sphere, z is equal to the square root of a negative number: no real solution exists. If that circle touches the sphere on exactly one point, z is equal to zero. If that circle touches the surface of the sphere at two points, then z is equal to plus or minus the square root of a positive number.

Preliminary and final computations

The Derivation section pointed out that the coordinate system in which the sphere centers are designated must be such that (1) all three centers are in the plane z = 0, (2) the sphere center, P1, is at the origin, and (3) the sphere center, P2, is on the x-axis. In general the problem will not be given in a form such that these requirements are met.

This problem can be overcome as described below where the points, P1, P2, and P3 are treated as vectors from the origin where indicated. P1, P2, and P3 are of course expressed in the original coordinate system.

${\hat {e}}_{x}={\frac {P2-P1}{\|P2-P1\|}}$ is the unit vector in the direction from P1 to P2.

$i={\hat {e}}_{x}\cdot (P3-P1)$ is the signed magnitude of the x component, in the figure 1 coordinate system, of the vector from P1 to P3.

${\hat {e}}_{y}={\frac {P3-P1-i\;{\hat {e}}_{x}}{\|P3-P1-i\;{\hat {e}}_{x}\|}}$ is the unit vector in the y direction. Note that the points P1, P2, and P3 are all in the z = 0 plane of the figure 1 coordinate system.

The third basis unit vector is ${\hat {e}}_{z}={\hat {e}}_{x}\times {\hat {e}}_{y}$. Therefore,

$d=\|P2-P1\|$ the distance between the centers P1 and P2 and

$j={\hat {e}}_{y}\cdot (P3-P1)$ is the signed magnitude of the y component, in the figure 1 coordinate system, of the vector from P1 to P3.

Using $i,\;d$ and $j$ as computed above, solve for x, y and z as described in the Derivation section. Then

${\vec {p}}_{1,2}=P1+x\ {\hat {e}}_{x}+y\ {\hat {e}}_{y}\ \pm \ z\ {\hat {e}}_{z}$

gives the points in the original coordinate system since ${\hat {e}}_{x},\;{\hat {e}}_{y}$ and ${\hat {e}}_{z}$, the basis unit vectors, are expressed in the original coordinate system.

See also

• Euclidean distance
• Multilateration – position estimation using measurements of time difference of arrival at (or from) three or more sites.
• Resection (orientation)
• Triangulation
• Global positioning system

References

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

External links

• Efficient Solution and Performance Analysis of 3-D Position Estimation by Trilateration