Invertible sheaf: Difference between revisions
en>David Eppstein →References: start not stub |
en>Addbot m Bot: Migrating 2 interwiki links, now provided by Wikidata on d:q2905137 |
||
| Line 1: | Line 1: | ||
'''Competitive inhibition''' is a form of [[enzyme inhibitor|enzyme inhibition]] where binding of the inhibitor to the active site on the [[enzyme]] prevents binding of the [[substrate (biochemistry)|substrate]] and ''vice versa''.<ref name="NIH CTT">{{cite web|title=Types of Inhibition|url=http://assay.nih.gov/assay/index.php/Types_of_Inhibition|publisher=NIH Center for Translational Therapeutics|accessdate=2 April 2012}}</ref><ref>{{cite web|title=Competitive Inhibition|url=http://cti.itc.virginia.edu/~cmg/Demo/compInh.html|accessdate=2 April 2012}}</ref> | |||
Most competitive inhibitors function by binding reversibly to the active site of the enzyme.<ref name="NIH CTT" /> As a result, many sources state that this is the defining feature of competitive inhibitors.<ref>{{cite web|title=Enzyme Inhibitors|url=http://www.elmhurst.edu/~chm/vchembook/573inhibit.html}}</ref><ref>{{cite web|title=Enzyme Inhibition|url=http://dl.clackamas.cc.or.us/ch106-08/enzyme1.htm|accessdate=2 April 2012}}</ref> This, however, is a misleading oversimplification, as there are many possible mechanisms by which an enzyme may bind either the inhibitor or the substrate but never both at the same time.<ref name="NIH CTT" /> For example, allosteric inhibitors may display competitive, [[non-competitive inhibition|non-competitive]], or [[uncompetitive inhibition|uncompetitive]] inhibition.<ref name="NIH CTT" /> | |||
==Mechanism== | |||
[[File:Comp inhib.svg|350px|Diagram showing competitive inhibition|right|thumb]] | |||
In competitive inhibition, at any given moment, the enzyme may be bound to the inhibitor, the substrate, or neither, but it cannot bind both at the same time. | |||
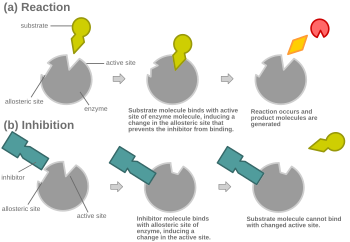
In virtually every case, competitive inhibitors bind in the same [[binding site]] as the substrate, but same-site binding is not a requirement. A competitive inhibitor could bind to an [[allosteric]] site of the free enzyme and prevent substrate binding, as long as it does not bind to the allosteric site when the substrate is bound. | |||
In competitive inhibition, the maximum velocity (<math>V_\max</math>) of the reaction is unchanged, while the apparent affinity of the substrate to the binding site is decreased (the <math>K_d</math> dissociation constant is apparently increased). The change in <math>K_m</math> ([[Michaelis-Menten]] constant) is parallel to the alteration in <math>K_d</math>. Any given competitive inhibitor concentration can be overcome by increasing the substrate concentration in which case the substrate will outcompete the inhibitor in binding to the enzyme. | |||
[[File:Allosteric comp inhib 1.svg|350px|Competitive inhibition can also be allosteric, as long as the inhibitor and the substrate cannot bind the enzyme at the same time.|thumb]] | |||
[[File:Allosteric comp inhib 2.svg|350px|Another possible mechanism for allosteric competitive inhibition.|thumb]] | |||
==Equation== | |||
Competitive inhibition increases the apparent value of the [[Michaelis-Menten]] constant, <math>K^\text{app}_m</math>, such that initial rate of reaction, <math>V_0</math>, is given by | |||
: <math> V_0 = \frac{V_\max\,[S]}{K^\text{app}_m + [S]}</math> | |||
where <math>K^\text{app}_m=K_m(1+[I]/K_i)</math>, <math>K_i</math> is the inhibitor's dissociation constant and <math>[I]</math> is the inhibitor concentration. | |||
<math>V_\max</math> remains the same because the presence of the inhibitor can be overcome by higher substrate concentrations. <math>K^\text{app}_m</math>, the substrate concentration that is needed to reach <math>V_\max / 2</math>, increases with the presence of a competitive inhibitor. This is because the concentration of substrate needed to reach <math>V_\max</math> with an inhibitor is greater than the concentration of substrate needed to reach <math>V_\max</math> without an inhibitor. | |||
==Derivation== | |||
In the simplest case of a single-substrate enzyme obeying Michaelis-Menten kinetics, the typical scheme | |||
:<math> | |||
E + S \, \overset{k_1}\underset{k_{-1}} \rightleftharpoons \, ES \, \overset{k_2} {\longrightarrow} \, E + P | |||
</math> | |||
is modified to include binding of the inhibitor to the free enzyme: | |||
:<math> | |||
EI + S \, \overset{k_{-3}}\underset{k_3} \rightleftharpoons \, E + S + I \, \overset{k_1}\underset{k_{-1}} \rightleftharpoons \, ES + I \, \overset{k_2} {\longrightarrow} \, E + P + I | |||
</math> | |||
Note that the inhibitor does not bind to the ES complex and the substrate does not bind to the EI complex. It is generally assumed that this behavior is indicative of both compounds binding at the same site, but that is not strictly necessary. As with the derivation of the Michaelis-Menten equation, assume that the system is at steady-state, i.e. the concentration of each of the enzyme species is not changing. | |||
: <math>\frac{d[E]}{dt} = \frac{d[ES]}{dt} = \frac{d[EI]}{dt} = 0. </math> | |||
Furthermore, the known total enzyme concentration is <math>[E]_0 = [E] + [ES] + [EI]</math>, and the velocity is measured under conditions in which the substrate and inhibitor concentrations do not change substantially and an insignificant amount of product has accumulated. | |||
We can therefore set up a system of equations: | |||
{{NumBlk|:|<math> [E]_0 = [E] + [ES] + [EI]\,\!</math>|{{EquationRef|1}}}} | |||
{{NumBlk|:|<math> \frac{d[E]}{dt} = 0 = -k_1[E][S] + k_{-1}[ES] + k_2[ES] -k_3[E][I] + k_{-3}[EI] </math>|{{EquationRef|2}}}} | |||
{{NumBlk|:|<math> \frac{d[ES]}{dt} = 0 = k_1[E][S] - k_{-1}[ES] - k_2[ES] </math>|{{EquationRef|3}}}} | |||
{{NumBlk|:|<math> \frac{d[EI]}{dt} = 0 = k_3[E][I] - k_{-3}[EI] </math>|{{EquationRef|4}}}} | |||
where <math>[S]</math>, <math>[I]</math> and <math>[E]_0</math> are known. The initial velocity is defined as <math>V_0 = d[P]/dt = k_2 [ES]</math>, so we need to define the unknown <math>[ES]</math> in terms of the knowns <math>[S]</math>, <math>[I]</math> and <math>[E]_0</math>. | |||
From equation ({{EquationNote|3}}), we can define ''E'' in terms of ''ES'' by rearranging to | |||
: <math> k_1[E][S]=(k_{-1}+k_2)[ES] \,\!</math> | |||
Dividing by <math>k_1[S]</math> gives | |||
: <math> [E] = \frac{(k_{-1}+k_2)[ES]}{k_1[S]} </math> | |||
As in the derivation of the Michaelis-Menten equation, the term <math>(k_{-1}+k_2)/k_1</math> can be replaced by the macroscopic rate constant <math>K_m</math>: | |||
{{NumBlk|:|<math> [E] = \frac{K_m[ES]}{[S]} </math>|{{EquationRef|5}}}} | |||
Substituting equation ({{EquationNote|5}}) into equation ({{EquationNote|4}}), we have | |||
: <math> 0 = \frac{k_3[I]K_m[ES]}{[S]} - k_{-3}[EI] </math> | |||
Rearranging, we find that | |||
: <math> [EI] = \frac{K_m k_3[I][ES]}{k_{-3}[S]} </math> | |||
At this point, we can define the dissociation constant for the inhibitor as <math>K_i = k_{-3}/k_3</math>, giving | |||
{{NumBlk|:|<math> [EI] = \frac{K_m[I][ES]}{K_i[S]}</math>|{{EquationRef|6}}}} | |||
At this point, substitute equation ({{EquationNote|5}}) and equation ({{EquationNote|6}}) into equation ({{EquationNote|1}}): | |||
: <math> [E]_0 = \frac{K_m[ES]}{[S]} + [ES] + \frac{K_m[I][ES]}{K_i[S]}</math> | |||
Rearranging to solve for ES, we find | |||
: <math> [E]_0 = [ES] \left ( \frac{K_m}{[S]} + 1 + \frac{K_m[I]}{K_i[S]} \right )= [ES] \frac{K_m K_i + K_i[S] + K_m[I]}{K_i[S]}</math> | |||
{{NumBlk|:|<math> [ES] = \frac{K_i [S][E]_0}{K_m K_i + K_i[S] + K_m[I]}</math>|{{EquationRef|7}}}} | |||
Returning to our expression for <math>V_0</math>, we now have: | |||
<math>\begin{align} | |||
V_0 & = k_2[ES] = \frac{k_2 K_i [S][E]_0}{K_m K_i + K_i[S] + K_m[I]} \\ | |||
& = \frac{k_2 [E]_0 [S]}{K_m + [S] + K_m\frac{[I]}{K_i}} | |||
\end{align} | |||
</math> | |||
Since the velocity is maximal when all the enzyme is bound as the enzyme-substrate complex, <math>V_\max = k_2 [E]_0</math>. | |||
Replacing and combining terms finally yields the conventional form: | |||
{{NumBlk|:|<math> V_0 = \frac{V_{\max}[S]}{K_m(1 + \frac{[I]}{K_i}) + [S]}</math>|{{EquationRef|8}}}} | |||
== References == | |||
{{reflist}} | |||
==See also== | |||
*[[Schild regression]] for ligand receptor inhibition | |||
*[[Non-competitive inhibition]] | |||
{{Enzyme inhibition}} | |||
{{DEFAULTSORT:Competitive Inhibition}} | |||
[[Category:Enzyme inhibitors]] | |||
Revision as of 04:40, 12 March 2013
Competitive inhibition is a form of enzyme inhibition where binding of the inhibitor to the active site on the enzyme prevents binding of the substrate and vice versa.[1][2]
Most competitive inhibitors function by binding reversibly to the active site of the enzyme.[1] As a result, many sources state that this is the defining feature of competitive inhibitors.[3][4] This, however, is a misleading oversimplification, as there are many possible mechanisms by which an enzyme may bind either the inhibitor or the substrate but never both at the same time.[1] For example, allosteric inhibitors may display competitive, non-competitive, or uncompetitive inhibition.[1]
Mechanism
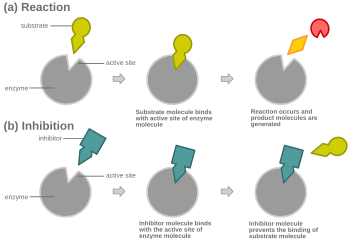
In competitive inhibition, at any given moment, the enzyme may be bound to the inhibitor, the substrate, or neither, but it cannot bind both at the same time.
In virtually every case, competitive inhibitors bind in the same binding site as the substrate, but same-site binding is not a requirement. A competitive inhibitor could bind to an allosteric site of the free enzyme and prevent substrate binding, as long as it does not bind to the allosteric site when the substrate is bound.
In competitive inhibition, the maximum velocity () of the reaction is unchanged, while the apparent affinity of the substrate to the binding site is decreased (the dissociation constant is apparently increased). The change in (Michaelis-Menten constant) is parallel to the alteration in . Any given competitive inhibitor concentration can be overcome by increasing the substrate concentration in which case the substrate will outcompete the inhibitor in binding to the enzyme.

Equation
Competitive inhibition increases the apparent value of the Michaelis-Menten constant, , such that initial rate of reaction, , is given by
where , is the inhibitor's dissociation constant and is the inhibitor concentration.
remains the same because the presence of the inhibitor can be overcome by higher substrate concentrations. , the substrate concentration that is needed to reach , increases with the presence of a competitive inhibitor. This is because the concentration of substrate needed to reach with an inhibitor is greater than the concentration of substrate needed to reach without an inhibitor.
Derivation
In the simplest case of a single-substrate enzyme obeying Michaelis-Menten kinetics, the typical scheme
is modified to include binding of the inhibitor to the free enzyme:
Note that the inhibitor does not bind to the ES complex and the substrate does not bind to the EI complex. It is generally assumed that this behavior is indicative of both compounds binding at the same site, but that is not strictly necessary. As with the derivation of the Michaelis-Menten equation, assume that the system is at steady-state, i.e. the concentration of each of the enzyme species is not changing.
Furthermore, the known total enzyme concentration is , and the velocity is measured under conditions in which the substrate and inhibitor concentrations do not change substantially and an insignificant amount of product has accumulated.
We can therefore set up a system of equations:
where , and are known. The initial velocity is defined as , so we need to define the unknown in terms of the knowns , and .
From equation (Template:EquationNote), we can define E in terms of ES by rearranging to
As in the derivation of the Michaelis-Menten equation, the term can be replaced by the macroscopic rate constant :
Substituting equation (Template:EquationNote) into equation (Template:EquationNote), we have
Rearranging, we find that
At this point, we can define the dissociation constant for the inhibitor as , giving
At this point, substitute equation (Template:EquationNote) and equation (Template:EquationNote) into equation (Template:EquationNote):
Rearranging to solve for ES, we find
Returning to our expression for , we now have:
Since the velocity is maximal when all the enzyme is bound as the enzyme-substrate complex, . Replacing and combining terms finally yields the conventional form:
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
See also
- Schild regression for ligand receptor inhibition
- Non-competitive inhibition





![{\displaystyle V_{0}={\frac {V_{\max }\,[S]}{K_{m}^{\text{app}}+[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e6ea985b759c13c54c08b2e1a1f7b292c549beb)
![{\displaystyle K_{m}^{\text{app}}=K_{m}(1+[I]/K_{i})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e013bb3d416acd07c0c55ee196d46e9ede190a63)

![{\displaystyle [I]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5962300a54e8ce8b5761dac9a5fbbca450c2ce0f)



![{\displaystyle {\frac {d[E]}{dt}}={\frac {d[ES]}{dt}}={\frac {d[EI]}{dt}}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/268777cfb0aa902787812bbb71d192f24b85464d)
![{\displaystyle [E]_{0}=[E]+[ES]+[EI]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97e7fcec01c7884f769ae9c075e6d1a4911f42d7)
![{\displaystyle [S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/292bbb82029aa583c5d2ac5fa1d7e4fedf537d8b)
![{\displaystyle [E]_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/409eb69aba4c3afa67a48af6d9f976a28445c544)
![{\displaystyle V_{0}=d[P]/dt=k_{2}[ES]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46255eb4443a618d59991823c0c26a019eb1422e)
![{\displaystyle [ES]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31639ab6b9c7c728139b5f8ce03991d800ac7741)
![{\displaystyle k_{1}[E][S]=(k_{-1}+k_{2})[ES]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81f920641b7d4ee0c9c57a53ebd2a43cca9cea0a)
![{\displaystyle k_{1}[S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f2a483dc97db9519f165c7f706ef334bddac55b)
![{\displaystyle [E]={\frac {(k_{-1}+k_{2})[ES]}{k_{1}[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daeace436c65cee7869e60b931f05cb1de334232)

![{\displaystyle 0={\frac {k_{3}[I]K_{m}[ES]}{[S]}}-k_{-3}[EI]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d54314972d85eabd9bb831f44a0737f4f7123e69)
![{\displaystyle [EI]={\frac {K_{m}k_{3}[I][ES]}{k_{-3}[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/668346ee94b193f238b09e941bcfe0a7ccc0fcfb)

![{\displaystyle [E]_{0}={\frac {K_{m}[ES]}{[S]}}+[ES]+{\frac {K_{m}[I][ES]}{K_{i}[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b2c23abf3e9cc29f2d34091e793b1b10fbcdde6)
![{\displaystyle [E]_{0}=[ES]\left({\frac {K_{m}}{[S]}}+1+{\frac {K_{m}[I]}{K_{i}[S]}}\right)=[ES]{\frac {K_{m}K_{i}+K_{i}[S]+K_{m}[I]}{K_{i}[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/195800a9b1300f606542d148f00b7e988ad3e2fa)
![{\begin{aligned}V_{0}&=k_{2}[ES]={\frac {k_{2}K_{i}[S][E]_{0}}{K_{m}K_{i}+K_{i}[S]+K_{m}[I]}}\\&={\frac {k_{2}[E]_{0}[S]}{K_{m}+[S]+K_{m}{\frac {[I]}{K_{i}}}}}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9353674da17993c18590af294421d9b31431fd45)
![{\displaystyle V_{\max }=k_{2}[E]_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d5602a3aa76c4c8e94949a07b8c7760704df376)