Reciprocity (photography): Difference between revisions
en>Michael Hardy mNo edit summary |
en>BattyBot m →History: fixed CS1 errors: dates & General fixes using AWB (9816) |
||
| Line 1: | Line 1: | ||
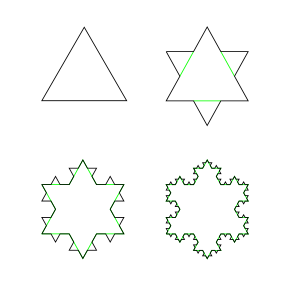
[[File:KochFlake.svg|thumb|right|Four stages in the construction of a [[Koch snowflake]]. As with many other [[fractal]]s, the stages are obtained via a recursive definition.]] | |||
A [[recursive definition]] (or '''inductive definition''') in [[mathematical logic]] and [[computer science]] is used to define an object in terms of itself (Aczel 1978:740ff). | |||
A recursive definition of a function defines values of the functions for some inputs in terms of the values of the same function for other inputs. For example, the [[factorial]] function ''n''! is defined by the rules | |||
:0! = 1. | |||
:(''n''+1)! = (''n''+1)·''n''!. | |||
This definition is valid for all ''n'', because the recursion eventually reaches the '''base case''' of 0. The definition may also be thought of as giving a procedure describing how to construct the function ''n''!, starting from n = 0 and proceeding onwards with n = 1, n = 2, n = 3 etc.. | |||
That such a definition indeed defines a function can be proved by induction. | |||
An inductive definition of a set describes the elements in a set in terms of other elements in the set. For example, one definition of the set '''N''' of [[natural number]]s is: | |||
#1 is in '''N'''. | |||
#If an element ''n'' is in '''N''' then ''n''+1 is in '''N'''. | |||
#'''N''' is the smallest set satisfying (1) and (2). | |||
There are many sets that satisfy (1) and (2) - for example, the set {1, 1.649, 2, 2.649, 3, 3.649, ...} satisfies the definition. However, condition (3) specifies the set of natural numbers by removing the sets with extraneous members. | |||
Properties of recursively defined functions and sets can often be proved by an [[mathematical induction|induction]] principle that follows the recursive definition. For example, the definition of the natural numbers presented here directly implies the '''principle of mathematical induction''' for natural numbers: if a property holds of the natural number 0, and the property holds of ''n''+1 whenever it holds of ''n'', then the property holds of all natural numbers (Aczel 1978:742). | |||
==Form of recursive definitions== | |||
Most recursive definition have three foundations: a base case (basis), an inductive clause, and an extremal clause. | |||
The difference between a [[circular definition]] and a recursive definition is that a recursive definition must always have ''base cases'', cases that satisfy the definition ''without'' being defined in terms of the definition itself, and all other cases comprising the definition must be "smaller" (''closer'' to those base cases that terminate the recursion) in some sense. In contrast, a circular definition may have no base case, and define the value of a function in terms of that value itself, rather than on other values of the function. Such a situation would lead to an [[infinite regress]]. | |||
==Proof that recursion defines a function== | |||
Suppose one has a pair of functions f and g on the natural numbers such that f(0)=0 and f(n+1)=g(f(n)) for all n. We want to construct, for any natural number n, a subset F(n) of N^2 such that: | |||
(1) for all natural numbers a between 0 and n: there exists a unique natural number b such that (a, b) is in F(n); | |||
(2) (0, f(0)) is in F(n); | |||
(3) for all natural numbers a, where a is between 0 and n-1: if (a, f(a)) is in F then (a+1, g(f(a))) is in F(n). | |||
Clearly {(0, f(0))} satisfies (2) and (3). | |||
Suppose these properties hold for n. Consider F(n+1)=F(n)U{(n,g(n))}. Then this set satisfies all 3 properties (1), (2), (3). By induction we have such a set for any natural number n. Let F be the set theoretic union of all the F(n), where the union is taken over all natural numbers n. | |||
==Examples of recursive definitions== | |||
===Elementary functions=== | |||
Addition is defined recursively based on counting | |||
:<math>0+a=a</math> | |||
:<math>(1+n)+a=1+(n+a)</math> | |||
Multiplication is defined recursively | |||
:<math>0 a=0</math> | |||
:<math>(1+n)a=a+na</math> | |||
Exponentiation is defined recursively | |||
:<math>a^0=1</math> | |||
:<math>a^{1+n}=a a^n</math> | |||
Binomial coefficients are defined recursively | |||
:<math>\binom{a}{0}=1</math> | |||
:<math>\binom{1+a}{1+n}=\frac{(1+a)\binom{a}{n}}{1+n}</math> | |||
===Prime numbers=== | |||
The set of [[prime number]]s can be defined as the unique set of positive integers satisfying | |||
* [[1 (number)|1]] is not a prime number | |||
* any other positive integer is a prime number if and only if it is not divisible by any prime number smaller than itself | |||
The primality of the integer 1 is the base case; checking the primality of any larger integer ''X'' by this definition requires knowing the primality of every integer between 1 and ''X'', which is well defined by this definition. That last point can proved by induction on ''X'', for which it is essential that the second clause says "if and only if"; if it had said just "if" the primality of for instance 4 would not be clear, and the further application of the second clause would be impossible. | |||
===Non-negative even numbers=== | |||
The [[even number]]s can be defined as consisting of | |||
* 0 is in the set E of non-negative evens (basis clause) | |||
* For any element x in the set E, x+2 is in E (inductive clause) | |||
* Nothing is in E unless it is obtained from the basis and inductive clauses (extremal clause). | |||
===Well formed formulas=== | |||
It is chiefly in logic or computer programming that recursive definitions are found. For example, a [[well formed formula]] (wff) can be defined as: | |||
#a symbol which stands for a [[proposition]] - like '''p''' means "Connor is a lawyer." | |||
#The negation symbol, followed by a wff - like '''Np''' means "It is not true that Connor is a lawyer." | |||
#Any of the four binary [[connective]]s (C, A, K, or E) followed by two wffs. The symbol '''K''' means "both are true", so '''Kpq''' may mean "Connor is a lawyer and Mary likes music." | |||
The value of such a recursive definition is that it can be used to determine whether any particular string of symbols is "well formed". | |||
* '''Kpq''' is well formed, because it's '''K''' followed by the atomic wffs '''p''' and '''q'''. | |||
* '''NKpq''' is well formed, because it's '''N''' followed by '''Kpq''', which is in turn a wff. | |||
* '''KNpNq''' is '''K''' followed by '''Np''' and '''Nq'''; and '''Np''' is a wff, etc. | |||
== See also == | |||
* [[Recursive data type]]s | |||
* [[Recursion]] | |||
* [[Mathematical induction]] | |||
== References == | |||
* P. Aczel (1977), "An introduction to inductive definitions", ''Handbook of Mathematical Logic'', J. Barwise (ed.), ISBN 0-444-86388-5 | |||
* James L. Hein (2009), ''Discrete Structures, Logic, and Computability''. ISBN 0-7637-7206-2 | |||
{{DEFAULTSORT:Recursive Definition}} | |||
[[Category:Definition]] | |||
[[Category:Mathematical logic]] | |||
[[Category:Theoretical computer science]] | |||
Revision as of 21:32, 29 December 2013
A recursive definition (or inductive definition) in mathematical logic and computer science is used to define an object in terms of itself (Aczel 1978:740ff).
A recursive definition of a function defines values of the functions for some inputs in terms of the values of the same function for other inputs. For example, the factorial function n! is defined by the rules
- 0! = 1.
- (n+1)! = (n+1)·n!.
This definition is valid for all n, because the recursion eventually reaches the base case of 0. The definition may also be thought of as giving a procedure describing how to construct the function n!, starting from n = 0 and proceeding onwards with n = 1, n = 2, n = 3 etc..
That such a definition indeed defines a function can be proved by induction.
An inductive definition of a set describes the elements in a set in terms of other elements in the set. For example, one definition of the set N of natural numbers is:
- 1 is in N.
- If an element n is in N then n+1 is in N.
- N is the smallest set satisfying (1) and (2).
There are many sets that satisfy (1) and (2) - for example, the set {1, 1.649, 2, 2.649, 3, 3.649, ...} satisfies the definition. However, condition (3) specifies the set of natural numbers by removing the sets with extraneous members.
Properties of recursively defined functions and sets can often be proved by an induction principle that follows the recursive definition. For example, the definition of the natural numbers presented here directly implies the principle of mathematical induction for natural numbers: if a property holds of the natural number 0, and the property holds of n+1 whenever it holds of n, then the property holds of all natural numbers (Aczel 1978:742).
Form of recursive definitions
Most recursive definition have three foundations: a base case (basis), an inductive clause, and an extremal clause.
The difference between a circular definition and a recursive definition is that a recursive definition must always have base cases, cases that satisfy the definition without being defined in terms of the definition itself, and all other cases comprising the definition must be "smaller" (closer to those base cases that terminate the recursion) in some sense. In contrast, a circular definition may have no base case, and define the value of a function in terms of that value itself, rather than on other values of the function. Such a situation would lead to an infinite regress.
Proof that recursion defines a function
Suppose one has a pair of functions f and g on the natural numbers such that f(0)=0 and f(n+1)=g(f(n)) for all n. We want to construct, for any natural number n, a subset F(n) of N^2 such that:
(1) for all natural numbers a between 0 and n: there exists a unique natural number b such that (a, b) is in F(n);
(2) (0, f(0)) is in F(n);
(3) for all natural numbers a, where a is between 0 and n-1: if (a, f(a)) is in F then (a+1, g(f(a))) is in F(n).
Clearly {(0, f(0))} satisfies (2) and (3).
Suppose these properties hold for n. Consider F(n+1)=F(n)U{(n,g(n))}. Then this set satisfies all 3 properties (1), (2), (3). By induction we have such a set for any natural number n. Let F be the set theoretic union of all the F(n), where the union is taken over all natural numbers n.
Examples of recursive definitions
Elementary functions
Addition is defined recursively based on counting
Multiplication is defined recursively
Exponentiation is defined recursively
Binomial coefficients are defined recursively
Prime numbers
The set of prime numbers can be defined as the unique set of positive integers satisfying
- 1 is not a prime number
- any other positive integer is a prime number if and only if it is not divisible by any prime number smaller than itself
The primality of the integer 1 is the base case; checking the primality of any larger integer X by this definition requires knowing the primality of every integer between 1 and X, which is well defined by this definition. That last point can proved by induction on X, for which it is essential that the second clause says "if and only if"; if it had said just "if" the primality of for instance 4 would not be clear, and the further application of the second clause would be impossible.
Non-negative even numbers
The even numbers can be defined as consisting of
- 0 is in the set E of non-negative evens (basis clause)
- For any element x in the set E, x+2 is in E (inductive clause)
- Nothing is in E unless it is obtained from the basis and inductive clauses (extremal clause).
Well formed formulas
It is chiefly in logic or computer programming that recursive definitions are found. For example, a well formed formula (wff) can be defined as:
- a symbol which stands for a proposition - like p means "Connor is a lawyer."
- The negation symbol, followed by a wff - like Np means "It is not true that Connor is a lawyer."
- Any of the four binary connectives (C, A, K, or E) followed by two wffs. The symbol K means "both are true", so Kpq may mean "Connor is a lawyer and Mary likes music."
The value of such a recursive definition is that it can be used to determine whether any particular string of symbols is "well formed".
- Kpq is well formed, because it's K followed by the atomic wffs p and q.
- NKpq is well formed, because it's N followed by Kpq, which is in turn a wff.
- KNpNq is K followed by Np and Nq; and Np is a wff, etc.
See also
References
- P. Aczel (1977), "An introduction to inductive definitions", Handbook of Mathematical Logic, J. Barwise (ed.), ISBN 0-444-86388-5
- James L. Hein (2009), Discrete Structures, Logic, and Computability. ISBN 0-7637-7206-2







