Ductility

The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology. Homomorphisms constructed with its help are generally called connecting homomorphisms.

Statement

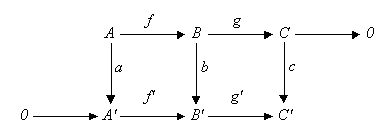
In an abelian category (such as the category of abelian groups or the category of vector spaces over a given field), consider a commutative diagram:

where the rows are exact sequences and 0 is the zero object. Then there is an exact sequence relating the kernels and cokernels of a, b, and c:

File:SnakeLemma02.png

Furthermore, if the morphism f is a monomorphism, then so is the morphism ker a → ker b, and if g' is an epimorphism, then so is coker b → coker c.

Explanation of the name

To see where the snake lemma gets its name, expand the diagram above as follows:

and then note that the exact sequence that is the conclusion of the lemma can be drawn on this expanded diagram in the reversed "S" shape of a slithering snake.

Construction of the maps

The maps between the kernels and the maps between the cokernels are induced in a natural manner by the given (horizontal) maps because of the diagram's commutativity. The exactness of the two induced sequences follows in a straightforward way from the exactness of the rows of the original diagram. The important statement of the lemma is that a connecting homomorphism d exists which completes the exact sequence.

In the case of abelian groups or modules over some ring, the map d can be constructed as follows. Pick an element x in ker c and view it as an element of C; since g is surjective, there exists y in B with g(y) = x. Because of the commutativity of the diagram, we have $g'(b(y))=c(g(y))=c(x)=0\!$ (since x is in the kernel of c), and therefore b(y) is in the kernel of g' . Since the bottom row is exact, we find an element z in A' with f '(z) = b(y). z is unique by injectivity of f '. We then define d(x) = z + im(a). Now one has to check that d is well-defined (i.e. d(x) only depends on x and not on the choice of y), that it is a homomorphism, and that the resulting long sequence is indeed exact.

Once that is done, the theorem is proven for abelian groups or modules over a ring. For the general case, the argument may be rephrased in terms of properties of arrows and cancellation instead of elements. Alternatively, one may invoke Mitchell's embedding theorem.

Naturality

In the applications, one often needs to show that long exact sequences are "natural" (in the sense of natural transformations). This follows from the naturality of the sequence produced by the snake lemma.

If

is a commutative diagram with exact rows, then the snake lemma can be applied twice, to the "front" and to the "back", yielding two long exact sequences; these are related by a commutative diagram of the form

In popular culture

• The proof of the snake lemma is being taught by Jill Clayburgh at the very beginning of the 1980 film It's My Turn.

See also

• List of lemmas

References

• Serge Lang: Algebra. 3rd edition, Springer 2002, ISBN 978-0-387-95385-4, pp. 157–159 (Template:Google books)
• M. F. Atiyah; I. G. Macdonald: Introduction to Commutative Algebra. Oxford 1969, Addison–Wesley Publishing Company, Inc. ISBN 0-201-00361-9.
• P. Hilton; U. Stammbach: A course in homological algebra. 2. Auflage, Springer Verlag, Graduate Texts in Mathematics, 1997, ISBN 0-387-94823-6, p. 99 (Template:Google books)

External links

• 
  
  I had like 17 domains hosted on single account, and never had any special troubles. If you are not happy with the service you will get your money back with in 45 days, that's guaranteed. But the Search Engine utility inside the Hostgator account furnished an instant score for my launched website. Fantastico is unable to install WordPress in a directory which already have any file i.e to install WordPress using Fantastico the destination directory must be empty and it should not have any previous installation files. When you share great information, others will take note. Once your hosting is purchased, you will need to setup your domain name to point to your hosting. Money Back: All accounts of Hostgator come with a 45 day money back guarantee. If you have any queries relating to where by and how to use Hostgator Discount Coupon, you can make contact with us at our site. If you are starting up a website or don't have too much website traffic coming your way, a shared plan is more than enough. Condition you want to take advantage of the worldwide web you prerequisite a HostGator web page, -1 of the most trusted and unfailing web suppliers on the world wide web today. Since, single server is shared by 700 to 800 websites, you cannot expect much speed.
  
  
  
  Hostgator tutorials on how to install Wordpress need not be complicated, especially when you will be dealing with a web hosting service that is friendly for novice webmasters and a blogging platform that is as intuitive as riding a bike. After that you can get Hostgator to host your domain and use the wordpress to do the blogging. Once you start site flipping, trust me you will not be able to stop. I cut my webmaster teeth on Control Panel many years ago, but since had left for other hosting companies with more commercial (cough, cough) interfaces. If you don't like it, you can chalk it up to experience and go on. First, find a good starter template design. When I signed up, I did a search for current "HostGator codes" on the web, which enabled me to receive a one-word entry for a discount. Your posts, comments, and pictures will all be imported into your new WordPress blog.
• Snake Lemma at PlanetMath
• Proof of the Snake Lemma in the film It's My Turn