Cryoscopic constant: Difference between revisions
en>ZéroBot m r2.7.1) (Robot: Adding ca:Constant crioscòpica |
No edit summary |
||
| Line 1: | Line 1: | ||
In [[probability theory]], two [[random variable]]s being [[Pearson product-moment correlation coefficient|uncorrelated]] does not imply their [[statistical independence|independence]]. In some contexts, uncorrelatedness implies at least [[pairwise independence]] (as when the random variables involved have [[Bernoulli distribution]]s). | |||
It is sometimes mistakenly thought that one context in which uncorrelatedness implies independence is when the random variables involved are [[normal distribution|normally distributed]]. However, this is incorrect if the variables are merely [[Marginal distribution|marginally]] normally distributed but not [[multivariate normal distribution|jointly normally distributed]]. | |||
Suppose two random variables ''X'' and ''Y'' are ''jointly'' normally distributed. That is the same as saying that the random vector (''X'', ''Y'') has a [[multivariate normal distribution]]. It means that the [[joint probability distribution]] of ''X'' and ''Y'' is such that each linear combination of ''X'' and ''Y'' is normally distributed, i.e. for any two constant (i.e., non-random) scalars ''a'' and ''b'', the random variable ''aX'' + ''bY'' is normally distributed. ''In that case'' if ''X'' and ''Y'' are uncorrelated, i.e., their [[covariance]] cov(''X'', ''Y'') is zero, ''then'' they are independent.<ref>{{cite book |title=Probability and Statistical Inference |year=2001 |last1=Hogg |first1=Robert |authorlink1=Robert Hogg |last2=Tanis |first2=Elliot | authorlink2=Elliot Tanis |edition=6th |chapter=Chapter 5.4 The Bivariate Normal Distribution |pages=258–259 |isbn=0130272949}}</ref> ''However'', it is possible for two random variables ''X'' and ''Y'' to be so distributed jointly that each one alone is marginally normally distributed, and they are uncorrelated, but they are not independent; examples are given below. | |||
==Examples== | |||
=== A symmetric example === | |||
[[File:uncorrelated sym.png|thumb|alt=Two normally distributed, uncorrelated but dependent variables.|Joint range of ''X'' and ''Y''. Darker indicates higher value of the density funtion.]] | |||
Suppose ''X'' has a normal distribution with [[expected value]] 0 and variance 1. Let ''W'' have the [[Rademacher distribution]], so that ''W'' = 1 or −1, each with probability 1/2, and assume ''W'' is independent of ''X''. Let ''Y'' = ''WX''. Then<ref>[http://www.math.uiuc.edu/~r-ash/Stat/StatLec21-25.pdf UIUC, Lecture 21. ''The Multivariate Normal Distribution''], 21.6:"Individually Gaussian Versus Jointly Gaussian".</ref> | |||
* ''X'' and ''Y'' are uncorrelated; | |||
* Both have the same normal distribution; and | |||
* ''X'' and ''Y'' are not independent. | |||
Note that the distribution of the simple linear combination ''X'' + ''Y'' concentrates positive probability at 0: Pr(''X'' + ''Y'' = 0) = 1/2 and so is not normally distributed. By the definition above, ''X'' and ''Y'' are not jointly normally distributed. | |||
To see that ''X'' and ''Y'' are uncorrelated, consider | |||
: <math> \begin{align} | |||
\operatorname{cov}(X,Y) &{} = E(XY) - E(X)E(Y) = E(XY) - 0 = E(E(XY\mid W)) \\ | |||
& {} = E(X^2)\Pr(W=1) + E(-X^2)\Pr(W=-1) \\ | |||
& {} = 1\cdot\frac12 + (-1)\cdot\frac12 = 0. | |||
\end{align} | |||
</math> | |||
To see that ''Y'' has the same normal distribution as ''X'', consider | |||
: <math>\begin{align} | |||
\Pr(Y \le x) & {} = E(\Pr(Y \le x\mid W)) \\ | |||
& {} = \Pr(X \le x)\Pr(W = 1) + \Pr(-X\le x)\Pr(W = -1) \\ | |||
& {} = \Phi(x) \cdot\frac12 + \Phi(x)\cdot\frac12 | |||
\end{align}</math> | |||
(since ''X'' and −''X'' both have the same normal distribution), where <math>\Phi(x)</math> is the [[cumulative distribution function]] of the normal distribution.. | |||
To see that ''X'' and ''Y'' are not independent, observe that |''Y''| = |''X''| or that Pr(''Y'' > 1 | ''X'' = 1/2) = 0. | |||
=== An asymmetric example === | |||
[[File:Uncorrelated asym.png|thumb|The joint density of X and Y. Darker indicates a higher value of the density.]] | |||
Suppose ''X'' has a normal distribution with [[expected value]] 0 and variance 1. Let | |||
: <math>Y=\left\{\begin{matrix} X & \text{if } \left|X\right| \leq c \\ | |||
-X & \text{if } \left|X\right|>c \end{matrix}\right.</math> | |||
where ''c'' is a positive number to be specified below. If ''c'' is very small, then the [[correlation]] corr(''X'', ''Y'') is near −1; if ''c'' is very large, then corr(''X'', ''Y'') is near 1. Since the correlation is a [[continuous function]] of ''c'', the [[intermediate value theorem]] implies there is some particular value of ''c'' that makes the correlation 0. That value is approximately 1.54. In that case, ''X'' and ''Y'' are uncorrelated, but they are clearly not independent, since ''X'' completely determines ''Y''. | |||
To see that ''Y'' is normally distributed—indeed, that its distribution is the same as that of ''X''—let us find its [[cumulative distribution function]]: | |||
: <math>\begin{align}\Pr(Y \leq x) &= \Pr(\{|X| \leq c\text{ and }X \leq x\}\text{ or }\{|X|>c\text{ and }-X \leq x\})\\ | |||
&= \Pr(|X| \leq c\text{ and }X \leq x) + \Pr(|X|>c\text{ and }-X \leq x)\\ | |||
&= \Pr(|X| \leq c\text{ and }X \leq x) + \Pr(|X|>c\text{ and }X \leq x) \\ | |||
&= \Pr(X \leq x). \end{align}\,</math> | |||
where the next-to-last equality follows from the symmetry of the distribution of ''X'' and the symmetry of the condition that |''X''| ≤ ''c''. | |||
Observe that the difference ''X'' − ''Y'' is nowhere near being normally distributed, since it has a substantial probability (about 0.88) of it being equal to 0, whereas the normal distribution, being a continuous distribution, has no discrete part, i.e., does not concentrate more than zero probability at any single point. Consequently ''X'' and ''Y'' are not ''jointly'' normally distributed, even though they are separately normally distributed.<ref>Edward L. Melnick and Aaron Tenenbein, "Misspecifications of the Normal Distribution", ''[[The American Statistician]]'', volume 36, number 4 November 1982, pages 372–373</ref> | |||
== References == | |||
{{reflist}} | |||
[[Category:Theory of probability distributions]] | |||
[[Category:Statistical dependence]] | |||
Revision as of 07:40, 7 January 2014
In probability theory, two random variables being uncorrelated does not imply their independence. In some contexts, uncorrelatedness implies at least pairwise independence (as when the random variables involved have Bernoulli distributions).
It is sometimes mistakenly thought that one context in which uncorrelatedness implies independence is when the random variables involved are normally distributed. However, this is incorrect if the variables are merely marginally normally distributed but not jointly normally distributed.
Suppose two random variables X and Y are jointly normally distributed. That is the same as saying that the random vector (X, Y) has a multivariate normal distribution. It means that the joint probability distribution of X and Y is such that each linear combination of X and Y is normally distributed, i.e. for any two constant (i.e., non-random) scalars a and b, the random variable aX + bY is normally distributed. In that case if X and Y are uncorrelated, i.e., their covariance cov(X, Y) is zero, then they are independent.[1] However, it is possible for two random variables X and Y to be so distributed jointly that each one alone is marginally normally distributed, and they are uncorrelated, but they are not independent; examples are given below.
Examples
A symmetric example
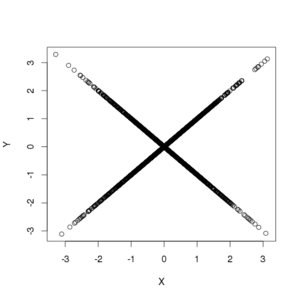
Suppose X has a normal distribution with expected value 0 and variance 1. Let W have the Rademacher distribution, so that W = 1 or −1, each with probability 1/2, and assume W is independent of X. Let Y = WX. Then[2]
- X and Y are uncorrelated;
- Both have the same normal distribution; and
- X and Y are not independent.
Note that the distribution of the simple linear combination X + Y concentrates positive probability at 0: Pr(X + Y = 0) = 1/2 and so is not normally distributed. By the definition above, X and Y are not jointly normally distributed.
To see that X and Y are uncorrelated, consider
To see that Y has the same normal distribution as X, consider
(since X and −X both have the same normal distribution), where is the cumulative distribution function of the normal distribution..
To see that X and Y are not independent, observe that |Y| = |X| or that Pr(Y > 1 | X = 1/2) = 0.
An asymmetric example

Suppose X has a normal distribution with expected value 0 and variance 1. Let
where c is a positive number to be specified below. If c is very small, then the correlation corr(X, Y) is near −1; if c is very large, then corr(X, Y) is near 1. Since the correlation is a continuous function of c, the intermediate value theorem implies there is some particular value of c that makes the correlation 0. That value is approximately 1.54. In that case, X and Y are uncorrelated, but they are clearly not independent, since X completely determines Y.
To see that Y is normally distributed—indeed, that its distribution is the same as that of X—let us find its cumulative distribution function:
where the next-to-last equality follows from the symmetry of the distribution of X and the symmetry of the condition that |X| ≤ c.
Observe that the difference X − Y is nowhere near being normally distributed, since it has a substantial probability (about 0.88) of it being equal to 0, whereas the normal distribution, being a continuous distribution, has no discrete part, i.e., does not concentrate more than zero probability at any single point. Consequently X and Y are not jointly normally distributed, even though they are separately normally distributed.[3]
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ UIUC, Lecture 21. The Multivariate Normal Distribution, 21.6:"Individually Gaussian Versus Jointly Gaussian".
- ↑ Edward L. Melnick and Aaron Tenenbein, "Misspecifications of the Normal Distribution", The American Statistician, volume 36, number 4 November 1982, pages 372–373




