Main Page: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
''' | :'' '''Incircle''' redirects here. For incircles of non-triangle polygons, see [[Tangential quadrilateral]] or [[Tangential polygon]]. | ||
[[Image:Incircle and Excircles.svg|right|thumb|300px|A triangle (black) with incircle (blue), [[incenter]] (I), excircles (orange), excenters (J<sub>A</sub>,J<sub>B</sub>,J<sub>C</sub>), internal [[angle bisector]]s (red) and external angle bisectors (green)]] | |||
In [[geometry]], the '''incircle''' or '''inscribed circle''' of a [[triangle]] is the largest [[circle]] contained in the triangle; it touches (is [[tangent]] to) the three sides. The center of the incircle is called the triangle's '''incenter'''. | |||
An '''excircle''' or '''escribed circle''' of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. | |||
Every triangle has three distinct excircles, each tangent to one of the triangle's sides. | |||
The center of the incircle can be found as the intersection of the three internal [[angle bisector]]s. | |||
The center of an excircle is the intersection of the internal bisector of one angle and the external bisectors of the other two. Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an [[orthocentric system]]. | |||
See also [[Tangent lines to circles]]. | |||
== Relation to area of the triangle == | |||
The radii of the incircles and excircles are closely related to the [[area]] of the triangle. Let ''A'' be the triangle's area and let ''a'', ''b'' and ''c'', be the lengths of its sides. By [[Heron's formula]], the area of the triangle is | |||
:<math> | |||
A=\frac{1}{4}\sqrt{P(a-b+c)(b-c+a)(c-a+b)}=\sqrt{s(s-a)(s-b)(s-c)} | |||
</math> | |||
where <math>s= \tfrac{1}{2}(a+b+c)</math> is the semiperimeter and <math>P = 2s</math> is the perimeter. | |||
The radius of the incircle (also known as the '''inradius''', ''r'' ) is | |||
: <math>r = \frac{2A}{P} = \sqrt{\frac{(s-a)(s-b)(s-c)}{s}}.</math> | |||
Thus, the area ''A'' of a triangle may be found by multiplying the inradius by the semiperimeter: | |||
:<math>\displaystyle A=rs.</math> | |||
</ | |||
The radii in the excircles are called the '''exradii'''. The excircle at side ''a'' has radius | |||
: <math>r_a = \frac{2A}{c-a+b} = \sqrt{\frac{s (s-b)(s-c)}{s-a}}.</math> | |||
Similarly the radii of the excircles at sides ''b'' and ''c'' are respectively | |||
: <math>r_b = \frac{2A}{a-b+c} = \sqrt{\frac{s (s-a)(s-c)}{s-b}}</math> | |||
and | |||
: <math>r_c = \frac{2A}{b-c+a} = \sqrt{\frac{s (s-a)(s-b)}{s-c}}.</math> | |||
From these formulas one can see that the excircles are always larger than the incircle and that the largest excircle is the one tangent to the longest side and the smallest excircle is tangent to the shortest side. Further, combining these formulas with Heron's area formula yields:<ref>Baker, Marcus, "A collection of formulae for the area of a plane triangle," ''Annals of Mathematics'', part 1 in vol. 1(6), January 1885, 134-138. (See also part 2 in vol. 2(1), September 1885, 11-18.)</ref> | |||
:<math>A=\sqrt{rr_ar_br_c}.</math> | |||
The ratio of the area of the incircle to the area of the triangle is less than or equal to <math>\frac{\pi}{3\sqrt{3}}</math>, with equality holding only for [[equilateral triangle]]s.<ref>Minda, D., and Phelps, S., "Triangles, ellipses, and cubic polynomials", ''[[American Mathematical Monthly]]'' 115, October 2008, 679-689: Theorem 4.1.</ref> | |||
== Nine-point circle and Feuerbach point == | |||
The circle tangent to all three of the excircles as well as the incircle is known as the [[nine-point circle]]. The point where the nine-point circle touches the incircle is known as the Feuerbach point. | |||
== Gergonne triangle and point == | |||
[[Image:Intouch Triangle and Gergonne Point.svg|right|frame|200px|A triangle, Δ''ABC'', with incircle (blue), incenter (blue, ''I''), contact triangle (red, Δ''T''<sub>''a''</sub>''T''<sub>''b''</sub>''T''<sub>''c''</sub>) and Gergonne point (green, Ge)]] | |||
The | The '''Gergonne triangle'''(of ''ABC'') is defined by the 3 touchpoints of the incircle on the 3 sides. | ||
Those vertices are denoted as ''T<sub>A</sub>'', etc. | |||
The point that ''T<sub>A</sub>'' denotes, lies opposite to ''A''. | |||
This '''Gergonne triangle''' ''T<sub>A</sub>T<sub>B</sub>T<sub>C</sub>'' is also known as the '''contact triangle''' or '''intouch triangle''' of ''ABC''. | |||
The three lines ''AT<sub>A</sub>'', ''BT<sub>B</sub>'' and ''CT<sub>C</sub>'' intersect in a single point called '''Gergonne point''', denoted as ''Ge'' - [[Triangle center|''X(7)'']]. | |||
== | Interestingly, the Gergonne point of a triangle is the [[symmedian point]] of the Gergonne triangle. For a full set of properties of the Gergonne point see.<ref>{{Cite journal | ||
| last = Dekov | |||
| first = Deko | |||
| title = Computer-generated Mathematics : The Gergonne Point | |||
| journal = Journal of Computer-generated Euclidean Geometry | |||
| year = 2009 | |||
| volume = 1 | |||
| pages = 1–14. | |||
| url = http://www.dekovsoft.com/j/2009/01/JCGEG200901.pdf}}</ref> | |||
The touchpoints of the three excircles with segments ''BC,CA and AB'' are the vertices of the [[extouch triangle]]. The points of intersection of the interior angle bisectors of ''ABC'' with the segments ''BC,CA,AB'' are the vertices of the '''incentral triangle'''. | |||
== Nagel triangle and point == | |||
The '''Nagel triangle''' of ''ABC'' is denoted by the vertices ''X<sub>A</sub>'', ''X<sub>B</sub>'' and ''X<sub>C</sub>'' that are the three points where the excircles touch the reference triangle ''ABC'' and where ''X<sub>A</sub>'' is opposite of ''A'', etc. This triangle ''X<sub>A</sub>X<sub>B</sub>X<sub>C</sub>'' is also known as the '''extouch triangle''' of ''ABC''. The circumcircle of the extouch triangle ''X<sub>A</sub>X<sub>B</sub>X<sub>C</sub>'' is called the '''Mandart circle'''. The three lines ''AX<sub>A</sub>'', ''BX<sub>B</sub>'' and ''CX<sub>C</sub>'' are called the [[Splitter (geometry)|splitters]] of the triangle; they each bisect the perimeter of the triangle, and they intersect in a single point, the triangle's [[Nagel point]] ''Na'' - [[Triangle center|''X(8)'']]. | |||
[[Trilinear coordinates]] for the vertices of the intouch triangle are given by | |||
*<math> A-\text{vertex}= 0 : \sec^2 \left(\frac{B}{2}\right) :\sec^2\left(\frac{C}{2}\right)</math> | |||
*<math> B-\text{vertex}= \sec^2 \left(\frac{A}{2}\right):0:\sec^2\left(\frac{C}{2}\right)</math> | |||
*<math> C-\text{vertex}= \sec^2 \left(\frac{A}{2}\right) :\sec^2\left(\frac{B}{2}\right):0</math> | |||
Trilinear coordinates for the vertices of the extouch triangle are given by | |||
* <math> A-\text{vertex} = 0 : \csc^2\left(\frac{B}{2}\right) : \csc^2\left(\frac{C}{2}\right)</math> | |||
* <math> B-\text{vertex} = \csc^2\left(\frac{A}{2}\right) : 0 : \csc^2\left(\frac{C}{2}\right)</math> | |||
* <math> C-\text{vertex} = \csc^2\left(\frac{A}{2}\right) : \csc^2\left(\frac{B}{2}\right) : 0</math> | |||
Trilinear coordinates for the vertices of the incentral triangle are given by | |||
* <math>\ A-\text{vertex} = 0 : 1 : 1</math> | |||
* <math>\ B-\text{vertex} = 1 : 0 : 1</math> | |||
* <math>\ C-\text{vertex} = 1 : 1 : 0</math> | |||
Trilinear coordinates for the vertices of the excentral triangle are given by | |||
* <math>\ A-\text{vertex}= -1 : 1 : 1 </math> | |||
* <math>\ B-\text{vertex}= 1 : -1 : 1 </math> | |||
* <math>\ C-\text{vertex}= 1 : -1 : -1 </math> | |||
Trilinear coordinates for the Gergonne point are given by | |||
: <math>\sec^2\left(\frac{A}{2}\right) : \sec^2 \left(\frac{B}{2}\right) : \sec^2\left(\frac{C}{2}\right)</math>, | |||
or, equivalently, by the [[Law of Sines]], | |||
: <math>\frac{bc}{b+ c - a} : \frac{ca}{c + a-b} : \frac{ab}{a+b-c}</math>. | |||
Trilinear coordinates for the Nagel point are given by | |||
: <math>\csc^2\left(\frac{A}{2}\right) : \csc^2 \left(\frac{B}{2}\right) : \csc^2\left(\frac{C}{2}\right)</math>, | |||
or, equivalently, by the [[Law of Sines]], | |||
: <math>\frac{b+ c - a}{a} : \frac{c + a-b}{b} : \frac{a+b-c}{c}</math>. | |||
It is the isotomic conjugate of the Gergonne point. | |||
==Coordinates of the incenter== | |||
The [[Cartesian coordinates]] of the incenter are a weighted average of the coordinates of the three vertices using the side lengths of the triangle as weights. (The weights are positive so the incenter lies inside the triangle as stated above.) If the three vertices are located at <math>(x_a,y_a)</math>, <math>(x_b,y_b)</math>, and <math>(x_c,y_c)</math>, and the sides opposite these vertices have corresponding lengths <math>a</math>, <math>b</math>, and <math>c</math>, then the incenter is at | |||
:<math>\bigg(\frac{a x_a+b x_b+c x_c}{P},\frac{a y_a+b y_b+c y_c}{P}\bigg) = \frac{a(x_a,y_a)+b(x_b,y_b)+c(x_c,y_c)}{P}</math> | |||
where <math>\ P = a + b + c.</math> | |||
[[Trilinear coordinates]] for the incenter are given by | |||
:<math>\ 1 : 1 : 1.</math> | |||
[[Barycentric coordinates (mathematics)|Barycentric coordinates]] for the incenter are given by | |||
:<math>\ a : b : c</math> | |||
or equivalently | |||
:<math>\sin(A):\sin(B):\sin(C).</math> | |||
==Equations for four circles== | |||
::<math> | Let x : y : z be a variable point in [[trilinear coordinates]], and let u = cos<sup>''2''</sup>''(A/2)'', v = cos<sup>''2''</sup>''(B/2)'', w = cos<sup>''2''</sup>''(C/2)''. The four circles described above are given by these equations: | ||
::<math> | :* Incircle: | ||
::<math>\ u^2x^2+v^2y^2+w^2z^2-2vwyz-2wuzx-2uvxy=0</math> | |||
::<math> | :* ''A-''excircle: | ||
::<math> u = 0 | ::<math>\ u^2x^2+v^2y^2+w^2z^2-2vwyz+2wuzx+2uvxy=0</math> | ||
:* ''B-''excircle: | |||
::<math>\ u^2x^2+v^2y^2+w^2z^2+2vwyz-2wuzx+2uvxy=0</math> | |||
:* ''C-''excircle: | |||
::<math>\ u^2x^2+v^2y^2+w^2z^2+2vwyz+2wuzx-2uvxy=0</math> | |||
==Euler's theorem== | |||
[[Euler's theorem in geometry|Euler's theorem]] states that in a triangle: | |||
:<math>(R-r_{in})^2=d^2+r_{in}^2,</math> | |||
where ''R'' and ''r''<sub>''in''</sub> are the circumradius and inradius respectively, and ''d'' is the distance between the circumcenter and the incenter. | |||
For excircles the equation is similar: | |||
:<math>(R+r_{ex})^2=d^2+r_{ex}^2,</math> | |||
where ''r''<sub>''ex''</sub> is the radius one of the excircles, and ''d'' is the distance between the circumcenter and this excircle's center. | |||
<ref name=Nelson>Nelson, Roger, "Euler's triangle inequality via proof without words," ''Mathematics Magazine'' 81(1), February 2008, 58-61.</ref> | |||
<ref>Johnson, R. A. ''Modern Geometry'', Houghton Mifflin, Boston, 1929: p. 187.</ref> | |||
<ref>[http://forumgeom.fau.edu/FG2001volume1/FG200120.pdf Emelyanov, Lev, and Emelyanova, Tatiana. "Euler’s formula and Poncelet’s porism", ''Forum Geometricorum'' 1, 2001: pp. 137–140.]</ref> | |||
== | ==Other incircle properties== | ||
Suppose the tangency points of the incircle divide the sides into lengths of ''x'' and ''y'', ''y'' and ''z'', and ''z'' and ''x''. Then the incircle has the radius<ref>Chu, Thomas, ''The Pentagon'', Spring 2005, p. 45, problem 584.</ref> | |||
:<math> r = \sqrt{\frac{xyz}{x+y+z}}</math> | |||
and the area of the triangle is | |||
:<math>K=\sqrt{xyz(x+y+z)}.</math> | |||
If the altitudes from sides of lengths ''a'', ''b'', and ''c'' are ''h<sub>a</sub>'', ''h<sub>b</sub>'', and ''h<sub>c</sub>'' then the inradius ''r'' is one-third of the harmonic mean of these altitudes, i.e. | |||
:<math> r = \frac{1}{h_a^{-1}+h_b^{-1}+h_c^{-1}}.</math> | |||
The product of the incircle radius ''r'' and the circumcircle radius ''R'' of a triangle with sides ''a'', ''b'', and ''c'' is<ref>Johnson, Roger A., ''Advanced Euclidean Geometry'', Dover, 2007 (orig. 1929), p. 189, #298(d).</ref> | |||
:<math>rR=\frac{abc}{2(a+b+c)}.</math> | |||
Some relations among the sides, incircle radius, and circumcircle radius are:<ref name=Bell/> | |||
:<math>ab+bc+ca=s^2+(4R+r)r,</math> | |||
:<math>a^2+b^2+c^2=2s^2-2(4R+r)r.</math> | |||
Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle.<ref>Kodokostas, Dimitrios, "Triangle Equalizers," ''Mathematics Magazine'' 83, April 2010, pp. 141-146.</ref> | |||
The distance from the incenter to the [[centroid]] is less than one third the length of the longest median of the triangle.<ref name=Franzsen>[http://forumgeom.fau.edu/FG2011volume11/FG201126.pdf Franzsen, William N.. "The distance from the incenter to the Euler line", ''Forum Geometricorum'' 11 (2011): 231–236.]</ref> | |||
Denoting the distance from the incenter to the Euler line as ''d'', the length of the longest median as ''v'', the length of the longest side as ''u'', and the semiperimeter as ''s'', the following inequalities hold:<ref name=Franzsen/> | |||
:<math>\frac{d}{s} < \frac{d}{u} < \frac{d}{v} < \frac{1}{3}.</math> | |||
Denoting the center of the incircle of triangle ''ABC'' as ''I'', we have<ref>Allaire, Patricia R.; Zhou, Junmin; and Yao, Haishen, "Proving a nineteenth century ellipse identity", ''[[Mathematical Gazette]]'' 96, March 2012, 161-165.</ref> | |||
:<math>\frac{\overline{IA} \cdot \overline{IA}}{\overline{CA} \cdot \overline{AB}} + \frac{\overline{IB} \cdot \overline{IB}}{\overline{AB} \cdot \overline{BC}} + \frac{\overline{IC} \cdot \overline{IC}}{\overline{BC} \cdot \overline{CA}} = 1.</math> | |||
==Other excircle properties== | |||
The circular [[convex hull|hull]] of the excircles is internally tangent to each of the excircles, and thus is an [[Problem of Apollonius|Apollonius circle]].<ref>[http://forumgeom.fau.edu/FG2002volume2/FG200222.pdf Grinberg, Darij, and Yiu, Paul, "The Apollonius Circle as a Tucker Circle", ''Forum Geometricorum'' 2, 2002: pp. 175-182.]</ref> The radius of this Apollonius circle is <math>\frac{r^2+s^2}{4r}</math> where ''r'' is the incircle radius and ''s'' is the semiperimeter of the triangle.<ref>[http://forumgeom.fau.edu/FG2003volume3/FG200320.pdf Stevanovi´c, Milorad R., "The Apollonius circle and related triangle centers", ''Forum Geometricorum'' 3, 2003, 187-195.]</ref> | |||
The following relations hold among the inradius ''r'', the circumradius ''R'', the semiperimeter ''s'', and the excircle radii ''r''<sub>'a''</sub>, ''r''<sub>''b''</sub>, ''r''<sub>''c''</sub>:<ref name=Bell>[http://forumgeom.fau.edu/FG2006volume6/FG200639.pdf Bell, Amy, "Hansen’s right triangle theorem, its converse and a generalization", ''Forum Geometricorum'' 6, 2006, 335–342.]</ref> | |||
:<math>r_a+r_b+r_c=4R+r,</math> | |||
:<math>r_a r_b+r_br_c+r_cr_a = s^2,</math> | |||
:<math>r_a^2 + r_b^2 + r_c^2 = (4R+r)^2 -2s^2,</math> | |||
The circle through the centers of the three excircles has radius 2''R''.<ref name=Bell/> | |||
If ''H'' is the [[orthocenter]] of triangle ''ABC'', then<ref name=Bell/> | |||
:<math>r_a+r_b+r_c+r=AH+BH+CH+2R,</math> | |||
:<math>r_a^2+r_b^2+r_c^2+r^2=AH^2+BH^2+CH^2+(2R)^2.</math> | |||
==Incircle in a quadrilateral== | |||
Some (but not all) [[quadrilateral]]s have an incircle. These are called [[tangential quadrilateral]]s. Among their many properties perhaps the most important is that their opposite sides have equal sums. This is called the [[Pitot theorem]]. | |||
== See also == | |||
*[[Altitude (triangle)]] | |||
*[[Circumscribed circle]] | |||
*[[Ex-tangential quadrilateral]] | |||
*[[Harcourt's theorem]] | |||
*[[Inscribed sphere]] | |||
*[[Power of a point]] | |||
*[[Steiner inellipse]] | |||
*[[Tangential quadrilateral]] | |||
*[[Triangle center]] | |||
==References== | ==References== | ||
{{reflist}} | {{reflist}} | ||
*Clark Kimberling, "Triangle Centers and Central Triangles," ''Congressus Numerantium'' 129 (1998) i-xxv and 1-295. | |||
*Sándor Kiss, "The Orthic-of-Intouch and Intouch-of-Orthic Triangles," ''Forum Geometricorum'' 6 (2006) 171-177. | |||
==External links== | ==External links== | ||
* [http://www. | * [http://www.mathalino.com/reviewer/derivation-of-formulas/derivation-of-formula-for-radius-of-incircle Derivation of formula for radius of incircle of a triangle] | ||
* {{MathWorld |title=Incircle |urlname=Incircle}} | |||
===Interactive=== | |||
*[http://www.mathopenref.com/triangleincenter.html Triangle incenter] [http://www.mathopenref.com/triangleincircle.html Triangle incircle] [http://www.mathopenref.com/polygonincircle.html Incircle of a regular polygon] With interactive animations | |||
*[http://www.mathopenref.com/constincircle.html Constructing a triangle's incenter / incircle with compass and straightedge] An interactive animated demonstration | |||
* [http://www.cut-the-knot.org/Curriculum/Geometry/AdjacentIncircles.shtml Equal Incircles Theorem] at [[cut-the-knot]] | |||
* [http://www.cut-the-knot.org/Curriculum/Geometry/FourIncircles.shtml Five Incircles Theorem] at [[cut-the-knot]] | |||
* [http://www.cut-the-knot.org/Curriculum/Geometry/IncirclesInQuadri.shtml Pairs of Incircles in a Quadrilateral] at [[cut-the-knot]] | |||
*[http://www.uff.br/trianglecenters/X0001.html An interactive Java applet for the incenter] | |||
{{DEFAULTSORT:Incircle And Excircles Of A Triangle}} | |||
[[Category: | [[Category:Circles]] | ||
[[Category: | [[Category:Triangle geometry]] | ||
[[de: | [[de:Inkreis]] | ||
Revision as of 08:05, 10 August 2014
- Incircle redirects here. For incircles of non-triangle polygons, see Tangential quadrilateral or Tangential polygon.
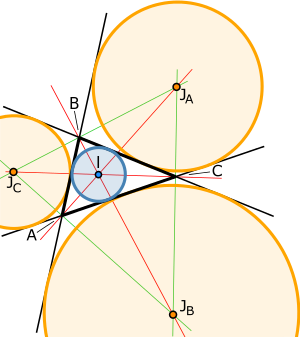
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is called the triangle's incenter.
An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides.
The center of the incircle can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle and the external bisectors of the other two. Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an orthocentric system.
See also Tangent lines to circles.
Relation to area of the triangle
The radii of the incircles and excircles are closely related to the area of the triangle. Let A be the triangle's area and let a, b and c, be the lengths of its sides. By Heron's formula, the area of the triangle is
where is the semiperimeter and is the perimeter.
The radius of the incircle (also known as the inradius, r ) is
Thus, the area A of a triangle may be found by multiplying the inradius by the semiperimeter:
The radii in the excircles are called the exradii. The excircle at side a has radius
Similarly the radii of the excircles at sides b and c are respectively
and
From these formulas one can see that the excircles are always larger than the incircle and that the largest excircle is the one tangent to the longest side and the smallest excircle is tangent to the shortest side. Further, combining these formulas with Heron's area formula yields:[1]
The ratio of the area of the incircle to the area of the triangle is less than or equal to , with equality holding only for equilateral triangles.[2]
Nine-point circle and Feuerbach point
The circle tangent to all three of the excircles as well as the incircle is known as the nine-point circle. The point where the nine-point circle touches the incircle is known as the Feuerbach point.
Gergonne triangle and point
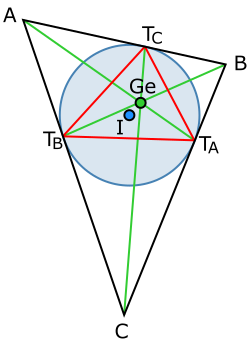
The Gergonne triangle(of ABC) is defined by the 3 touchpoints of the incircle on the 3 sides. Those vertices are denoted as TA, etc. The point that TA denotes, lies opposite to A.
This Gergonne triangle TATBTC is also known as the contact triangle or intouch triangle of ABC.
The three lines ATA, BTB and CTC intersect in a single point called Gergonne point, denoted as Ge - X(7).
Interestingly, the Gergonne point of a triangle is the symmedian point of the Gergonne triangle. For a full set of properties of the Gergonne point see.[3]
The touchpoints of the three excircles with segments BC,CA and AB are the vertices of the extouch triangle. The points of intersection of the interior angle bisectors of ABC with the segments BC,CA,AB are the vertices of the incentral triangle.
Nagel triangle and point
The Nagel triangle of ABC is denoted by the vertices XA, XB and XC that are the three points where the excircles touch the reference triangle ABC and where XA is opposite of A, etc. This triangle XAXBXC is also known as the extouch triangle of ABC. The circumcircle of the extouch triangle XAXBXC is called the Mandart circle. The three lines AXA, BXB and CXC are called the splitters of the triangle; they each bisect the perimeter of the triangle, and they intersect in a single point, the triangle's Nagel point Na - X(8).
Trilinear coordinates for the vertices of the intouch triangle are given by
Trilinear coordinates for the vertices of the extouch triangle are given by
Trilinear coordinates for the vertices of the incentral triangle are given by
Trilinear coordinates for the vertices of the excentral triangle are given by
Trilinear coordinates for the Gergonne point are given by
or, equivalently, by the Law of Sines,
Trilinear coordinates for the Nagel point are given by
or, equivalently, by the Law of Sines,
It is the isotomic conjugate of the Gergonne point.
Coordinates of the incenter
The Cartesian coordinates of the incenter are a weighted average of the coordinates of the three vertices using the side lengths of the triangle as weights. (The weights are positive so the incenter lies inside the triangle as stated above.) If the three vertices are located at , , and , and the sides opposite these vertices have corresponding lengths , , and , then the incenter is at
Trilinear coordinates for the incenter are given by
Barycentric coordinates for the incenter are given by
or equivalently
Equations for four circles
Let x : y : z be a variable point in trilinear coordinates, and let u = cos2(A/2), v = cos2(B/2), w = cos2(C/2). The four circles described above are given by these equations:
Euler's theorem
Euler's theorem states that in a triangle:
where R and rin are the circumradius and inradius respectively, and d is the distance between the circumcenter and the incenter.
For excircles the equation is similar:
where rex is the radius one of the excircles, and d is the distance between the circumcenter and this excircle's center. [4] [5] [6]
Other incircle properties
Suppose the tangency points of the incircle divide the sides into lengths of x and y, y and z, and z and x. Then the incircle has the radius[7]
and the area of the triangle is
If the altitudes from sides of lengths a, b, and c are ha, hb, and hc then the inradius r is one-third of the harmonic mean of these altitudes, i.e.
The product of the incircle radius r and the circumcircle radius R of a triangle with sides a, b, and c is[8]
Some relations among the sides, incircle radius, and circumcircle radius are:[9]
Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle.[10]
The distance from the incenter to the centroid is less than one third the length of the longest median of the triangle.[11]
Denoting the distance from the incenter to the Euler line as d, the length of the longest median as v, the length of the longest side as u, and the semiperimeter as s, the following inequalities hold:[11]
Denoting the center of the incircle of triangle ABC as I, we have[12]
Other excircle properties
The circular hull of the excircles is internally tangent to each of the excircles, and thus is an Apollonius circle.[13] The radius of this Apollonius circle is where r is the incircle radius and s is the semiperimeter of the triangle.[14]
The following relations hold among the inradius r, the circumradius R, the semiperimeter s, and the excircle radii r'a, rb, rc:[9]
The circle through the centers of the three excircles has radius 2R.[9]
If H is the orthocenter of triangle ABC, then[9]
Incircle in a quadrilateral
Some (but not all) quadrilaterals have an incircle. These are called tangential quadrilaterals. Among their many properties perhaps the most important is that their opposite sides have equal sums. This is called the Pitot theorem.
See also
- Altitude (triangle)
- Circumscribed circle
- Ex-tangential quadrilateral
- Harcourt's theorem
- Inscribed sphere
- Power of a point
- Steiner inellipse
- Tangential quadrilateral
- Triangle center
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- Clark Kimberling, "Triangle Centers and Central Triangles," Congressus Numerantium 129 (1998) i-xxv and 1-295.
- Sándor Kiss, "The Orthic-of-Intouch and Intouch-of-Orthic Triangles," Forum Geometricorum 6 (2006) 171-177.
External links
- Derivation of formula for radius of incircle of a triangle
I had like 17 domains hosted on single account, and never had any special troubles. If you are not happy with the service you will get your money back with in 45 days, that's guaranteed. But the Search Engine utility inside the Hostgator account furnished an instant score for my launched website. Fantastico is unable to install WordPress in a directory which already have any file i.e to install WordPress using Fantastico the destination directory must be empty and it should not have any previous installation files. When you share great information, others will take note. Once your hosting is purchased, you will need to setup your domain name to point to your hosting. Money Back: All accounts of Hostgator come with a 45 day money back guarantee. If you have any queries relating to where by and how to use Hostgator Discount Coupon, you can make contact with us at our site. If you are starting up a website or don't have too much website traffic coming your way, a shared plan is more than enough. Condition you want to take advantage of the worldwide web you prerequisite a HostGator web page, -1 of the most trusted and unfailing web suppliers on the world wide web today. Since, single server is shared by 700 to 800 websites, you cannot expect much speed.
Hostgator tutorials on how to install Wordpress need not be complicated, especially when you will be dealing with a web hosting service that is friendly for novice webmasters and a blogging platform that is as intuitive as riding a bike. After that you can get Hostgator to host your domain and use the wordpress to do the blogging. Once you start site flipping, trust me you will not be able to stop. I cut my webmaster teeth on Control Panel many years ago, but since had left for other hosting companies with more commercial (cough, cough) interfaces. If you don't like it, you can chalk it up to experience and go on. First, find a good starter template design. When I signed up, I did a search for current "HostGator codes" on the web, which enabled me to receive a one-word entry for a discount. Your posts, comments, and pictures will all be imported into your new WordPress blog.
Interactive
- Triangle incenter Triangle incircle Incircle of a regular polygon With interactive animations
- Constructing a triangle's incenter / incircle with compass and straightedge An interactive animated demonstration
- Equal Incircles Theorem at cut-the-knot
- Five Incircles Theorem at cut-the-knot
- Pairs of Incircles in a Quadrilateral at cut-the-knot
- An interactive Java applet for the incenter
- ↑ Baker, Marcus, "A collection of formulae for the area of a plane triangle," Annals of Mathematics, part 1 in vol. 1(6), January 1885, 134-138. (See also part 2 in vol. 2(1), September 1885, 11-18.)
- ↑ Minda, D., and Phelps, S., "Triangles, ellipses, and cubic polynomials", American Mathematical Monthly 115, October 2008, 679-689: Theorem 4.1.
- ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ Nelson, Roger, "Euler's triangle inequality via proof without words," Mathematics Magazine 81(1), February 2008, 58-61.
- ↑ Johnson, R. A. Modern Geometry, Houghton Mifflin, Boston, 1929: p. 187.
- ↑ Emelyanov, Lev, and Emelyanova, Tatiana. "Euler’s formula and Poncelet’s porism", Forum Geometricorum 1, 2001: pp. 137–140.
- ↑ Chu, Thomas, The Pentagon, Spring 2005, p. 45, problem 584.
- ↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover, 2007 (orig. 1929), p. 189, #298(d).
- ↑ 9.0 9.1 9.2 9.3 Bell, Amy, "Hansen’s right triangle theorem, its converse and a generalization", Forum Geometricorum 6, 2006, 335–342.
- ↑ Kodokostas, Dimitrios, "Triangle Equalizers," Mathematics Magazine 83, April 2010, pp. 141-146.
- ↑ 11.0 11.1 Franzsen, William N.. "The distance from the incenter to the Euler line", Forum Geometricorum 11 (2011): 231–236.
- ↑ Allaire, Patricia R.; Zhou, Junmin; and Yao, Haishen, "Proving a nineteenth century ellipse identity", Mathematical Gazette 96, March 2012, 161-165.
- ↑ Grinberg, Darij, and Yiu, Paul, "The Apollonius Circle as a Tucker Circle", Forum Geometricorum 2, 2002: pp. 175-182.
- ↑ Stevanovi´c, Milorad R., "The Apollonius circle and related triangle centers", Forum Geometricorum 3, 2003, 187-195.
























































