(+)-Camphor 6-endo-hydroxylase
Whereas all constraints in a constraint satisfaction problem (CSP) must be satisfied, a Weighted Constraint Satisfaction Problem (WCSP) is a constraint satisfaction problem where constraints can be violated (according a violation degree) and in which preferences among solutions can be expressed. Many real problems can be represented as Constraint Satisfaction Problem. However, a wide range of problems are over-constrained (no solution can be found without violating at least one constraint) or have multiple solutions and the goal is to find the solution having minimal cost according to a cost function. This kind of Constraint Satisfaction Problem are called Weighted Constraint Satisfaction Problem (WCSP).
Formal definition
A Weighted Constraint Network (WCN) is a triplet where is a finite set of variables, is a finite set of soft constraints and >0 is either a natural integer or .
Each soft constraint involves an ordered set of variables, called its scope, and is defined as a cost function from to where is the set of possible instantiations of . When an instantiation is given the cost , i.e., , it is said forbidden. Otherwise it is permitted with the corresponding cost (0 being completely satisfactory).
In WCSP, specific subclass of Valued CSP (VCSP), costs are combined with the specific operator defined as: . The partial inverse of is defined by: if , and if , .
Without any loss of generality, the existence of a nullary constraint (a cost) as well as the presence of a unary constraint for every variable is assumed.
The total cost of an instantiation on a soft constraint , includes the cost of on as well as the nullary cost and the unary costs for of the variables in .
Considering a WCN, the usual (NP-hard) task of WCSP is to find a complete instantiation with a minimal cost.
Resolution of binary/ternary WCSPs
Approach with cost transfer operations
Node consistency (NC) and Arc consistency (AC), introduced for the Constraint Satisfaction Problem (CSP), have been studied later in the context of WCSP. Furthermore, several consistencies about the best form of arc consistency have been proposed: Full Directional Arc consistency (FDAC),[1] Existencial Directional Arc consistency (EDAC),[2] Virtual Arc consistency (VAC)[3] and Optimal Soft Arc consistency (OSAC).[4]
Algorithms enforcing such properties are based on Equivalence Preserving Transformations (EPT) that allow safe moves of costs among constraints. Three basic costs transfer operations are:
- Project : cost transfer from constraints to unary constraints
- ProjectUnary : cost transfer from unary constraint to nullary constraint
- Extend : cost transfer from unary constraint to constraint
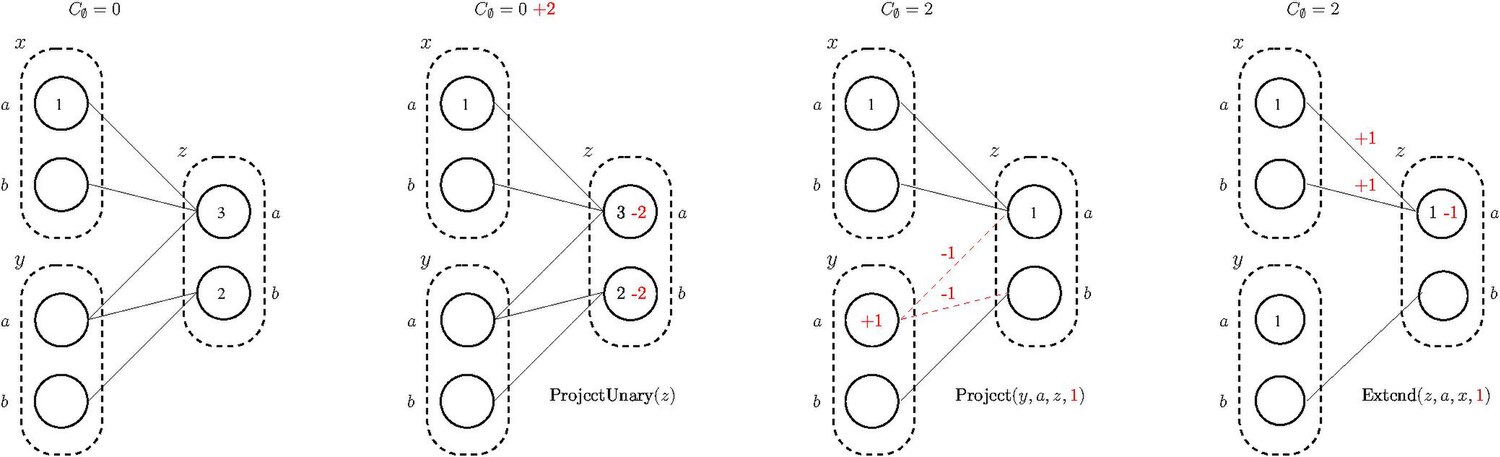
The goal of Equivalence Preserving Transformations is to concentrate costs on the nullary constraint and remove efficiently instantiations and values with a cost, additionned to , that is greater than or equal to the forbidden cost or the cost of the best solution found
Approach without cost transfer operations
An alternative to cost transfer algorithms is the algorithm PFC-MRDAC[5] which is a classical branch and bound algorithm that computes lower bound at each node of the search tree, that corresponds to an under-estimation of the cost of any solution that can be obtained from this node. The cost of the best solution found is . When , then the search tree from this node is pruned.
Resolution of n-ary WCSPs
Cost transfer algorithms have been shown to be particularly efficient to solve real-world problem when soft constraints are binary or ternary (maximal arity of constraints in the problem is equal to 2 or 3). For soft constraints of large arity, cost transfer becomes a serious issue because the risk of combinatorial explosion has to be controlled.
An algorithm, called ,[6] has been proposed to enforce a weak version of the property Generalized Arc Consistency (GAC) on soft constraints defined extensionally by listing tuples and their costs. This algorithm combine two techniques, namely, Simple Tabular Reduction (STR)[7] and cost transfer. Values that are no longer consistent with respect to GAC are identify and minimum costs of values are computed, which is particularly useful for performing efficiently projection operations that are required to establish GAC.
Benchmarks
Many real-world WCSP benchmarks are available on http://costfunction.org/en/benchmark[8] and on http://www.cril.univ-artois.fr/~lecoutre/benchmarks.html.
See also
- Constraint Satisfaction Problem
- Constraint satisfaction problem
- Programmation par contraintes
- Problème de satisfaction de contrainte
References
- ↑ M. Cooper. Reduction operations in fuzzy or valued constraint satisfaction. Fuzzy Sets and Systems, 134(3):311–342, 2003.
- ↑ S. de Givry, F. Heras, M. Zytnicki, and J. Larrosa. Existential arc consistency: Getting closer to full arc consistency in weighted CSPs. In Proceedings of IJCAI’05, pages 84–89, 2005.
- ↑ M. Cooper, S. de Givry, M. Sanchez, T. Schiex, M. Zytnicki. Virtual Arc Consistency for Weighted CSP. In Proceedings of AAAI’08, pages 253-258, 2008.
- ↑ M. Cooper, S. de Givry, M. Sanchez, T. Schiex, M. Zytnicki, and T. Werner. Soft arc consistency revisited. Artificial Intelligence, 174(7-8):449–478, 2010.
- ↑ E.C. Freuder and R.J. Wallace. Partial constraint satisfaction. Artificial Intelligence, 58(1- 3):21–70, 1992.
- ↑ C. Lecoutre, N. Paris, O. Roussel, S. Tabary. Propagating Soft Table Constraints. In Proceedings of CP’12, pages 390-405, 2012.
- ↑ C. Lecoutre. STR2: Optimized simple tabular reduction for table constraint. Constraints, 16(4):341–371, 2011.
- ↑ The aims of this web site is to promote cost function network in providing Benchmark and teaching material, solver demo, link to articule about cost function used in the contexte of constraint programming.