Complex dimension
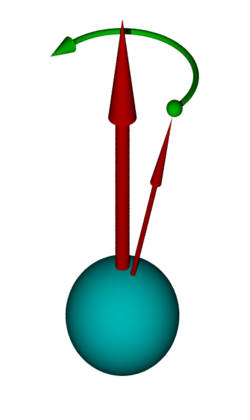
In physics, Larmor precession (named after Joseph Larmor) is the precession of the magnetic moments of electrons, muons, all leptons with magnetic moments which are quantum effects of particle spin, atomic nuclei, and atoms about an external magnetic field. The magnetic field exerts a torque on the magnetic moment,
where is the torque, is the magnetic dipole moment, is the angular momentum vector, is the external magnetic field, symbolizes the cross product, and is the gyromagnetic ratio which gives the proportionality constant between the magnetic moment and the angular momentum.
Larmor frequency
The angular momentum vector precesses about the external field axis with an angular frequency known as the Larmor frequency,
where is the angular frequency,[1] is the gyromagnetic ratio, and is the magnitude of the magnetic field[2] and is the g-factor (normally 1, except in quantum physics).
Simplified, this becomes:
where is the Larmor frequency, m is mass, e is charge, and B is applied field. For a given nucleus, the g-factor includes the effects of the spin of the nucleons as well as their orbital angular momentum and the coupling between the two. Because the nucleus is so complicated, g factors are very difficult to calculate, but they have been measured to high precision for most nuclei. Each nuclear isotope has a unique Larmor frequency for NMR spectroscopy, which is tabulated here.
Including Thomas precession
The above equation is the one that is used in most applications. However, a full treatment must include the effects of Thomas precession, yielding the equation (in CGS units):
where is the relativistic gamma factor (not to be confused with the gyromagnetic ratio above). Notably, for the electron g is very close to 2 (2.002..), so if one sets g=2, one arrives at
Bargmann–Michel–Telegdi equation
The spin precession of an electron in an external electromagnetic field is described by the Bargmann–Michel–Telegdi (BMT) equation [3]
where , , , and are polarization four-vector, charge, mass, and magnetic moment, is four-velocity of electron, , , and is electromagnetic field-strength tensor. Using equations of motion,
one can rewrite the first term in the right side of the BMT equation as , where is four-acceleration. This term describes Fermi–Walker transport and leads to Thomas precession. The second term is associated with Larmor precession.
When electromagnetic fields are uniform in space or when gradient forces like can be neglected, the particle's translational motion is described by
The BMT equation is then written as [4]
The Beam-Optical version of the Thomas-BMT, from the Quantum Theory of Charged-Particle Beam Optics, applicable in accelerator optics [5] [6]
Applications
A 1935 paper published by Lev Landau and Evgeny Lifshitz predicted the existence of ferromagnetic resonance of the Larmor precession, which was independently verified in experiments by J. H. E. Griffiths (UK) and E. K. Zavoiskij (USSR) in 1946.
Larmor precession is important in nuclear magnetic resonance, electron paramagnetic resonance and muon spin resonance. It is also important for the alignment of cosmic dust grains, which is a cause of the polarization of starlight.
To calculate the spin of a particle in a magnetic field, one must also take into account Thomas precession.
Precession direction
The precession direction is determined by the chirality of the particle.
See also
Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
External links
- ↑ Spin Dynamics, Malcolm H. Levitt, Wiley, 2001
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ V. Bargmann, L. Michel, and V. L. Telegdi, Precession of the Polarization of Particles Moving in a Homogeneous Electromagnetic Field, Phys. Rev. Lett. 2, 435 (1959).
- ↑ Jackson, J. D., Classical Electrodynamics, 3rd edition, Wiley, 1999, p. 563.
- ↑ M. Conte, R. Jagannathan, S. A. Khan and M. Pusterla, Beam optics of the Dirac particle with anomalous magnetic moment, Particle Accelerators, 56, 99-126 (1996); (Preprint: IMSc/96/03/07, INFN/AE-96/08).
- ↑ Khan, S. A. (1997). Quantum Theory of Charged-Particle Beam Optics, Ph.D Thesis, University of Madras, Chennai, India. (complete thesis available from Dspace of IMSc Library, The Institute of Mathematical Sciences, where the doctoral research was done).