LCP array
Template:Distinguish Polyhalogen ions are a group of polyatomic cations and anions containing halogens only. The ions can be classified into two classes, isopolyhalogen ions which contain one type of halogen only, and heteropolyhalogen ions with more than one type of halogen.
Introduction
Numerous polyhalogen ions have been found, with their salts isolated in the solid state and structurally characterized. The following tables summarize the species found so far.[1][2][3][4][5]
| Isopolyhalogen cations | |
|---|---|
| Diatomic species | *[Cl2]+, [Br2]+, [I2]+ |
| Triatomic species | [Cl3]+, [Br3]+, [I3]+ |
| Tetraatomic species | [Cl4]+, [I4]2+ |
| Pentaatomic species | [Br5]+, [I5]+ |
| Heptaatomic species | ^[I7]+ |
| Higher species | [I15]3+ |
Notes: *[Cl2]+ can only exist as [Cl2O2]2+ at low temperatures, a charge-transfer complex from O2 to [Cl2]+.[2] Free [Cl2]+ is only known from its electronic band spectrum obtained in a low-pressure discharge tube.[3] ^The existence of [I7]+ is possible but still uncertain.[1]
| Heteropolyhalogen cations | |
|---|---|
| Triatomic species | [ClF2]+, [Cl2F]+, [BrF2]+, [IF2]+, [ICl2]+, [IBrCl]+, [IBr2]+, [I2Cl]+, [I2Br]+ |
| Pentaatomic species | [ClF4]+, [BrF4]+, [IF4]+, [I3Cl2]+ |
| Heptaatomic species | [ClF6]+, [BrF6]+, [IF6]+ |
| Isopolyhalogen anions | |
|---|---|
| Triatomic species | [Cl3]-, [Br3]-, [I3]- |
| Tetraatomic species | [Br4]2-, [I4]2- |
| Pentaatomic species | [I5]- |
| Heptaatomic species | [I7]- |
| Octaatomic species | [Br8]2-, [I8]2- |
| Higher species | [I9]-, [I10]2-, [I10]4-, [I11]-, [I12]2-, [I13]3-, [I16]2-, [I22]4-, [I26]3-, [I26]4-, [I28]4-, [I29]3- |
| Heteropolyhalogen anions | |
|---|---|
| Triatomic species | [ClF2]-, [BrF2]-, [BrCl2]-, [IF2]-, [ICl2]-, [IBrF]-, [IBrCl]-, [IBr2]-, [I2Cl]-, [I2Br]-, [AtBrCl]-, [AtBr2]-, [AtICl]-, [AtIBr]-, [AtI2]- |
| Pentaatomic species | [ClF4]-, [BrF4]-, [IF4]-, [ICl3F]-, [ICl4]-, [IBrCl3]-, [I2Cl3]-, [I2BrCl2]-, [I2Br2Cl]-, [I2Br3]-,[I4Cl]-, [I4Br]- |
| Hexaatomic species | [IF5]2- |
| Heptaatomic species | [ClF6]-, [BrF6]-, [IF6]-, [I3Br4]- |
| Nonaatomic species | [IF8]- |
Structure




Most of the structures of the ions have been determined by IR spectroscopy, Raman spectroscopy and X-ray crystallography. The polyhalogen ions always have the heaviest and least electronegative halogen present in the ion as the central atom, making the ion asymmetric in some cases. For example, [Cl2F]+ has a structure of [Cl–Cl–F]- but not [Cl–F–Cl]-.
In general, the structures of most heteropolyhalogen ions and lower isopolyhalogen ions were in agreement with the VSEPR model. However, there were exceptional cases. For example, when the central atom is heavy and has seven lone pairs, such as [BrF6]- and [IF6]-, they have an regular octahedral arrangement of fluoride ligands instead of a distorted one due to the presence of a stereochemically inert lone pair. More deviations from the ideal VSEPR model were found in the solid state structures due to strong cation-anion interactions, which also complicates interpretation of vibrational spectroscopic data. In fact, all known structures of the polyhalogen anion salts, the anions make very close contact, via halogen bridges, with the counter-cations.[4] For example, in the solid state, [IF6]- is not regularly octahedral, as solid state structure of [Me4N]+[IF6]- reveals loosely bound [I2F11]2- dimers. Significant cation-anion interactions were also found in [BrF2]+[SbF6]-, [ClF2]+[SbF6]-, [BrF4]+[Sb6F11]-.[2]
| General structures of selected heteropolyhalogen ions | |
|---|---|
| Linear (or almost linear) | [ClF2]-, [BrF2]-, [BrCl2]-, [IF2]-, [ICl2]-, [IBr2]-, [I2Cl]-, [I2Br]- |
| Bent | [ClF2]+, [Cl2F]+, [BrF2]+, [IF2]+, [ICl2]+, [I2Cl]+, [IBr2]+, [I2Br]+, [IBrCl]+ |
| Square planar | [ClF4]-, [BrF4]-, [IF4]-, [ICl4]- |
| Disphenoidal (or seesaw) | [ClF4]+, [BrF4]+, [IF4]+ |
| Pentagonal planar | #[IF5]2- |
| Octahedral | [ClF6]+, [BrF6]+, [IF6]+, §[ClF6]-, [BrF6]-, [IF6]- |
| Square antiprismatic | [IF8]- |
Note: #[IF5]2- is one of the two XYn-type species known to have the rare pentagonal planar geometry, the other being [XeF5]-. §[ClF6]- is distorted octahedral as the stereochemical inert pair effect is not significant in the chlorine atom.
The [I3Cl2]+ and [I3Br2]+ ions have a trans-Z-type structure, analogous to that of [I5]+.
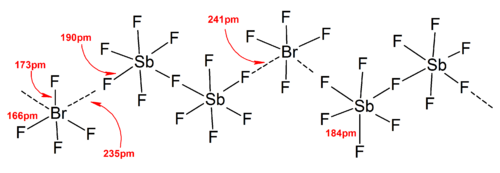
Higher polyiodides
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
The polyiodide ions have much more complicated structures. Discrete polyiodides usually have a linear sequence of iodine atoms and iodide ions, and is described in terms of association between I2, I- and I3- units, which reflects the origin of the polyiodide. In the solid states, the polyiodides can interact with each other to form chains, rings, or even complicated two-dimensional and three-dimensional networks.
Bonding
The bonding in polyhalogen ions mostly invoke the predominant use of p-orbitals. Significant d-orbital participation in the bonding is improbable as much promotional energy will be required, while scant s-orbital participation is expected in iodine-containing species due to the inert pair effect, suggested by data from Mössbauer spectroscopy. However, no bonding model has been capable of reproducing such wide range of bond lengths and angles observed so far.[3]
As expected from the fact that an electron is removed from the antibonding orbital when X2 is ionized to [X2]+, the bond order as well as the bond strength in [X2]+ gets higher, consequently the interatomic distances in the molecular ion is less than those in X2.
Linear or nearly linear triatomic polyhalides have weaker and longer bonds compared with that in the corresponding diatomic interhalogen or halogen, consistent with the additional repulsion between atoms as the halide ion is added to the neutral molecule. Another model involving the use of resonance theory exists, for example, [ICl2]- can be viewed as the resonance hybrid of the following canonical forms:
Evidence supporting this theory comes from the bond lengths (255pm in [ICl2]- and 232pm in ICl(g)) and bond stretching wavenumbers (267 and 222 cm−1 for symmetric and asymmetric stretching in [ICl2]- compared with 384 cm−1 in ICl), which suggests a bond order of about for each I–Cl bonds in [ICl2]-, consistent with the interpretation using the resonance theory. Other triatomic species [XY2]- can be similarly interpreted.[2]
Synthesis
The formation of polyhalogen ions can be viewed as the self-dissociation of their parent interhalogens or halogens:
- 2 XYn Template:Eqm [XYn-1]+ + [XYn+1]-
- 3 X2 Template:Eqm [X3]+ + [X3]-
- 4 X2 Template:Eqm [X5]+ + [X3]-
- 5 X2 Template:Eqm 2 [X2]+ + 2 [X3]-
Polyhalogen cations
There are two general strategies for preparing polyhalogen cations:
- By reacting the appropriate interhalogen with a lewis acid (such as the halides of B, Al, P, As, Sb) either in an inert or oxidizing solvent (such as anhydrous HF) or without one, to give a heteropolyhalogen cation.
- XYn + MYm → [XYn-1]+ + [MYm+1]-
- By an oxidative process, in which the halogen or interhalogen is reacted with an oxidizer and a lewis acid to give the cation:
- Cl2 + ClF + AsF5 → [Cl3]+[AsF6]-
In some cases the lewis acid (the fluoride acceptor) itself act as an oxidant:
- 3 I2 + 3 SbF5 → 2 [I3]+[SbF6]- + SbF3
Usually the first method is employed for preparing heteropolyhalogen cations, and the second one is applicable to both. The oxidative process is useful in the preparation of the cations [IBr2]+, [ClF6]+, [BrF6]+, as their parent interhalogens, IBr3, ClF7, BrF7 respectively, has never been isolated:
- Br2 + IOSO2F → [IBr2]+[SO3F]-
- 2 ClF5 + 2 PtF6 → [ClF6]+[PtF6]- + [ClF4]+[PtF6]-
- BrF5 + [KrF]+[AsF6]- → [BrF6]+[AsF6]- + Kr
The preparation of some individual species are briefly summarized in the table below with equations:[1][2][3][4]
| Synthesis of some polyhalogen cations | ||
|---|---|---|
| Species | Relevant chemical equation | Additional conditions required |
| [Cl2]+ (as [Cl2O2]+) | Cl2 + [O2]+[SbF6]- → [Cl2O2]+[SbF6]- | in anhydrous HF at low temperatures |
| [Br2]+ | Br2 (in BrSO3F) + 3 SbF5 → [Br2]+[Sb3F16]- (not balanced) | at room temperature |
| [I2]+ | 2 I2 + S2O6F2 → 2 [I2]+[SO3F]- | in HSO3F |
| [Cl3]+ | Cl2 + ClF + AsF5 → [Cl3]+[AsF6]- | at a temperature of 195K |
| [Br3]+ | 3 Br2 + 2 [O2]+[AsF6]- → 2 [Br3]+[AsF6]- + 2 O2 | |
| [I3]+ | 3 I2 + S2O6F2 → 2 [I3]+[SO3F]- | |
| [Cl4]+ | 2 Cl2 + IrF6 → [Cl4]+[IrF6]- | in anhydrous HF, at a temperature of <193K |
| [I4]2+ | 2 I2 + 3 AsF5 → [I4]2+[AsF6-]2 + AsF3 | in liquid SO2 |
| [Br5]+ | 8 Br2 + 3 [XeF]+[AsF6]- → 3 [Br5]+[AsF6]- + 3 Xe + BrF3 | |
| [I5]+ | 2 I2 + ICl + AlCl3 → [I5]+[AlCl4]- | |
| [I7]+ | 7 I2 + S2O6F2 → 2 I7SO3F | |
| [ClF2]+ | ClF3 + AsF5 → [ClF2]+[AsF6]- | |
| [Cl2F]+ | 2 ClF + AsF5 → [Cl2F]+[AsF6]- | at a temperature of <197K |
| [BrF2]+ | 5 BrF3 + 2 Au → 3 BrF + 2 [BrF2]+[AuF4]- | with excess BrF3 required |
| [IF2]+ | IF3 + AsF5 → [IF2]+[AsF6]- | |
| [ICl2]+ | ICl3 + SbCl5 → [ICl2]+[SbCl6]- | |
| [IBr2]+ | Br2 + IOSO2F → [IBr2]+[SO3F]- | |
| [ClF4]+ | ClF5 + SbF5 → [ClF4]+[SbF6]- | |
| [BrF4]+ | BrF5 + AsF5 → [BrF4]+[AsF6]- | |
| [IF4]+ | IF5 + 2 SbF5 → [IF4]+[Sb2F11]- | |
| [ClF6]+ | ‡Cs2NiF6 + 5 AsF5 + ClF5 → [ClF6]+[AsF6]- + Ni[AsF6]2 + 2 CsAsF6 | |
| [BrF6]+ | [KrF]+[AsF6]- + BrF5 → [BrF6]+[AsF6]- + Kr | |
| [IF6]+ | IF7 + BrF3 → [IF6]+[BrF4]- | |
‡In this reaction, the active oxidizing species is [NiF3]+, which is formed in situ in the Cs2NiF6/AsF5/HF system. It is an even more powerful oxidizing and fluorinating agent than PtF6.
Polyhalogen anions
For polyhalogen anions, there are two general preparation strategies as well:
- By reacting an interhalogen or halogen with a lewis base, most likely a fluoride:
- [Et4N]+Y- + XYn → [Et4N]+[XYn+1]-
- X2 + X- → X3-
- By oxidation of simple halides:
- KI + Cl2 → K+[ICl2]-
The preparation of some individual species are briefly summarized in the table below with equations:[1][2][3][4]
| Synthesis of some polyhalogen anions | ||
|---|---|---|
| Species | Relevant chemical equation | Additional conditions required |
| [Cl3]-, [Br3]-, [I3]- | X2 + X- → [X3]- (X = Cl, Br, I) | |
| [Br3]- | Br2 + [nBu4N]+Br- → [nBu4N]+[Br3]- | in 1,2-dichloroethane or liquid sulfur dioxide. [Br3]- does not exist in solution and is only formed when the salt crystallizes out. |
| [Br5]- | 2 Br2 + [nBu4N]+Br- → [nBu4N]+[Br5]- | in 1,2-dichloroethane or liquid sulfur dioxide, with excess Br2 |
| [ClF2]- | ClF + CsF → Cs+[ClF2]- | |
| [BrCl2]-[6] | Br2 + Cl2 + 2 CsCl → 2 Cs+[BrCl2]- | |
| [ICl2]-[7] | KI + Cl2 → K+[ICl2]- | |
| [IBr2]-[8] | CsI + Br2 → Cs+[IBr2]- | |
| [AtBr2]-, [AtICl]-, [AtIBr]-, [AtI2]- | AtY + X- → [AtXY]- (X = I, Br, Cl; Y = I, Br) | |
| [ClF4]- | NOF + ClF3 → [NO]+[ClF4]- | |
| [BrF4]- | 6 KCl + 8 BrF3 → 6 K+[BrF4]- + 3 Cl2 + Br2 | excess BrF5 needed |
| [IF4]- | 2 XeF2 + [Me4N]+I- → [Me4N]+[IF4]- + 2 Xe | the reactants were mixed at 242K, then warmed to 298K for the reaction to proceed |
| [ICl4]-[9] | KI + ICl3 → K+[ICl4]- | |
| [IF5]2- | IF3 + 2 [Me4N]+F- → [Me4N+]2[IF5]2- | |
| [IF6]- | IF5 + CsF → Cs+[IF6]- | |
| [I3Br4]- | [PPh4]+Br- + 3 IBr → [PPh4]+[I3Br4]- | |
| [IF8]- | IF7 + [Me4N]+F- → [Me4N]+[IF8]- | in acetonitrile |
The higher polyiodides were formed upon crystallization of solutions containing various concentrations of I- and I2. For instance, the monohydrate of KI3 crystallizes when a saturated solution containing appropriate amounts of I2 and KI is cooled.[10]
Properties
Stability
In general, a large counter cation or anion (such as Cs+, [SbF6]-) can help stabilize the polyhalogen ions formed in the solid state from lattice energy considerations, as the packing efficiency was increased.
The polyhalogen cations are strong oxidizing agents, as indicated by the fact that they can only be prepared in oxidative liquids as a solvent, such as oleum. The most oxidizing and therefore most unstable ones are the species [X2]+ and [XF6]+ (X = Cl, Br), followed by [X3]+ and [IF6]+.
The stability of the [X2]+ salts (X = Br, I) are thermodynamically quite stable. However, their stability in solution depends on the superacid solvent. For example, [I2]+ is stable in HF of highest highest acidity (HF with 0.2N SbF5, H0 = -20.65), but disproportionates to [I3]+, [I5]+ and I2 as acidity is decreased by adding different amounts of NbF5, TaF5 or NaF.[4]
- 14 [I2]+ + 5 F- → 9 [I3]+ + IF5
For polyhalogen anions with the same cation, the more stable ones are those with a heavier halogen at the center, symmetric ions are also more stable than asymmetric ones. therefore the stability of the anions decrease in the order:
- [I3]- > [IBr2]- > [ICl2]- > [I2Br]- > [Br3]- > [BrCl2]- > [Br2Cl]-
Heteropolyhalogen ions with a coordination number larger than or equal to four can only exist with fluoride ligands.
Color
Most polyhalogen ions are intensely colored, with deepened color as the atomic weight of the constituent element increases. The well-known starch-iodine complex has a deep blue color due to the linear [I5]- ions present in the amylose helix.[4] Some colors of the common species were listed below:[3]
- fluorocations tend to be colorless or pale yellow, other heteropolyhalogen ions are orange, red or deep purple[4]
- compounds of [ICl2]+ are wine red to bright orange; while that of [I2Cl]+ are dark brown to purplish black
- [Cl3]+ is yellow
- [Cl4]+ is blue[2]
- [Br2]+ is cherry red
- [Br3]+ is brown
- [Br5]+ is dark brown
- [I2]+ is bright blue
- [I3]+ is dark brown to black
- [I4]2+ is red to brown
- [I5]+ is green or black, the salt [I5]+[AlCl4]- exists as greenish-black needles, but appears brown-red in thin sections
- [I7]+ is black, if its existence in the compound I7SO3F has been firmly established
- [I15]3+ is black[5]
- [ICl4]- is golden-yellow
- polyiodides have very dark colors, either dark brown or dark blue
Chemical properties
The heteropolyhalogen cations are explosively reactive oxidants, and the cations often have higher reactivity than their parent interhalogens and decompose by reductive pathways. As expected from the highest oxidation state of +7 in [ClF6]+, [BrF6]+ and [IF6]+, these species are extremely strong oxidizing agents, demonstrated by the reactions shown below:
Polyhalogen cations with lower oxidation states tend to disproportionate. For example, [Cl2F]+ is unstable in solution and disproportionate completely in HF/SbF5 even at 197K:
- 2 [Cl2F]+ → [ClF2]+ + [Cl3]+
[I2]+ reversibly dimerizes at 193K, and is observed as the blue color of paramagnetic [I2]+ dramatically shifts to the red-brown color of diamagnetic [I2]+, together with a drop in paramagnetic susceptibility and electrical conductivity when the solution is cooled to below 193K:[2]
- 2 [I2]+ Template:Eqm [I4]2+
The dimerization can be attributed to the overlapping of the half-filled π* orbitals in two [I2]+.
[Cl4]+ in [Cl4]+[IrF6]- is structurally analogous to [I4]2+, but decomposes at 195K to give salts of [Cl3]+ instead of [Cl2]+ and Cl2.[2]
Attempts to prepare ClF7 and BrF7 by fluorinating [ClF6]+ and [BrF6]+ using NOF have met with failure, instead the following reactions occurred:[3]
- [ClF6]+[PtF6]- + NOF →[NO]+[PtF6]- + ClF5 + F2
- [BrF6]+[AsF6]- + 2 NOF →[NO]+[AsF6]- + [NO]+[BrF6]- + F2
The anions are less reactive compared to the cations, and are generally weaker oxidants than their parent interhalogens. They are less reactive towards organic compounds, and some salts are of quite high thermal stability. Salts containing polyhalogen anions of the type M+[XmYnZp]- (where m+n+p = 3, 5, 7, 9...) tend to dissociate into simple monohalide salts between M+ and the most electronegative halogen, so that the monohalide has the highest lattice energy. An interhalogen is usually formed as the other product. The salt [Me4N]+[ClF4]- decomposes at about 100°C, and salts of [ClF6]- are thermally unstable and can explode even at -31°C.[4]
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- ↑ 1.0 1.1 1.2 1.3 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Welcome to NewLaunch101.com. Buying a property is rarely a straightforward decision in life, and we do perceive that. To be able to help buyers/consumers out to be more conscious of the current market situation and the accessible options to select from, that is why NewLaunch101.com was created.
Government wealth taxation generally takes the form of both taxes on capital positive factors and/or estate duties. Any tax coverage must strike a stability between socially-acceptable wealth creation and extreme wealth accumulation. Bangkok is Thailand's top tourist destination and it is an awesome city. However should you just like the seashore, the seaside resort of Hua Hin is simply three hours by car from Bangkok. This picturesque town has great shopping, cool eating places, relaxing cafés, and contemporary seafood you could purchase right off the boat. There may be also mountain climbing and camping, world-class golf programs, and delightful beaches and islands on your doorstep. From Cambodia to Thailand-Take pleasure in a Low Cost of Living in Asia ABSD for Residential Properties Declaration For m (one hundred seventy five KB)
The truth is, things can get pretty chaotic, with buyers clamouring to be the first to e book their models. For some Singapore property gross sales, there might even be overnight queues. To keep away from that, developers may select to use balloting as a substitute of queueing for determining who will get to enter the showflat first. a) SSD at 15% if the property is offered within the first 12 months of purchase, i.e. the property is held for one year or much less from the date of purchase b) SSD at 10% if the property is sold in the second yr of buy, i.e. the property is held for multiple yr and as much as two years from the date of buy. Any non-standard clauses from the Sale & Purchase Settlement (the ultimate contract for the sale - see under); The sale that price ready for
BG Tan has had a distinguished profession with the SAF for over 26 years, during which he held important command and staff appointments requiring strong leadership, analytical, and organisational abilities. These included Future Methods Architect, Commander, third Singapore Division and Assistant Chief of the General Employees (Intelligence). BG Tan will retire from the SAF and return to the Administrative Service with effect from 1 June 2011. In Singapore, a developer who needs to promote models in an uncompleted growth, such as one that has simply began building, must first obtain a Sale License to do so. The Venue Residences to Stay, Store and Dine, a luxurious mixeddevelopment by CDL in preparation for launch now. Looking for registrationof curiosity.
Nevertheless, the newest cooling measure s seemed to have really taken the wind out from the sails of the property market. With a tightened loan to worth (LTV) framework and the introduction of the Total Debt Servicing Ratio (TDSR), speculators and investors not discover it as enticing to simply purchase into any property for a quick profit. Thus, property costs and transaction volumes have started to slip. The new property tax schedule for owner-occupied houses will be certain that most retirees will end up paying decrease property taxes, he added. Imposed on Everlasting Residents (PRs) purchasing their first residential property and on Singaporeans buying their second residential property. Citizenship ABSD Fee on Why do we solely have property tax as a wealth tax?
Rising workplace sector leads real property market efficiency, whereas prime retail and enterprise park segments average and residential sector continues in decline Latest knowledge from Actual Capital Analytics (RCA) exhibits real property advisory firm suggested on the most offers by value within the area in 2013 A substitute for estate duties is an inheritance tax, which assesses beneficiaries rather than the property of the deceased, and may be simpler to manage and accumulate, notably when assets are held overseas. There isn't a purpose for an organization or particular person not to buy. Don't ask me why they pay lease. A few of them pay even rent to overseas homeowners or overseas owned firms. District 18, 999 yr LH residence Residential items & fifty seven business models Posted by Edison Foo July 3, 2013
Singapore new launches, new Landed Home, Cluster Home, Apartment, House, Business Industrial Properties for Sale New Initiatives Launched ! Simply click on > B uying E nquiry just under this annoucement to register your interest with us for selection models booking. You'll be able to obtain Website Plans and Flooring Plans from Learn More under singapore new condo launches Launch Initiatives. However, for HDB upgraders getting another HDB flat or HDB government condominium, the monthly cost under the existing property could be excluded from the debt-servicing calculation. That is provided the present property is present process the sale course of, and the borrowers don't own every other property (including joint ownership with others) or have any other property loans to their title. RiverParc EC @ Punggol - ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 5.0 5.1 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ "Cesium dichlorobromide" in Handbook of Preparative Inorganic Chemistry, 2nd Ed. Edited by G. Brauer, Academic Press, 1963, NY. Vol. 1. p. 294.
- ↑ "Potassium dichloroiodide" in Handbook of Preparative Inorganic Chemistry, 2nd Ed. Edited by G. Brauer, Academic Press, 1963, NY. Vol. 1. p. 295.
- ↑ "Cesium dibromoiodide" in Handbook of Preparative Inorganic Chemistry, 2nd Ed. Edited by G. Brauer, Academic Press, 1963, NY. Vol. 1. p. 297.
- ↑ "Potassium tetrachloroiodide" in Handbook of Preparative Inorganic Chemistry, 2nd Ed. Edited by G. Brauer, Academic Press, 1963, NY. Vol. 1. p. 298.
- ↑ "Potassium triiodide" in Handbook of Preparative Inorganic Chemistry, 2nd Ed. Edited by G. Brauer, Academic Press, 1963, NY. Vol. 1. p. 294.
