Lyapunov vector
Template:Use mdy dates In open channel flow, specific energy (E) is the energy length, or head, relative to the channel bottom. Specific energy is expressed in terms of kinetic energy, and potential energy, and internal energy. The Bernoulli equation, which originates from a control volume analysis, is used to describe specific energy relationships in fluid dynamics. The form of Bernoulli’s equation discussed here assumes the flow is incompressible and steady. The three energy components in Bernoulli's equation are elevation, pressure and velocity. However, since with open channel flow, the water surface is open to the atmosphere, the pressure term between two points has the same value and is therefore ignored. Thus, if the specific energy and the velocity of the flow in the channel are known, the depth of flow can be determined. This relationship can be used to calculate changes in depth upstream or downstream of changes in the channel such as steps, constrictions, or control structures. It is also the fundamental relationship used in the Standard Step Method to calculate how the depth of a flow changes over a reach from the energy gained or lost due to the slope of the channel.
Introduction
With the pressure term neglected, energy exists in two forms, potential and kinetic. Assuming all the fluid particles are moving at the same velocity, the general expression for kinetic energy applies (KE = ½mv2). This general expression can be written in terms of kinetic energy per unit weight of fluid,
Where: m = mass v = fluid velocity (length/time) V = volume (length3) ρ = fluid density (mass/volume) γ = specific weight of water (weight/unit volume) g = acceleration due to gravity (length/time2)
The kinetic energy, in feet, is represented as the velocity head,
The fluid particles also have potential energy, which is associated with the fluid elevation above an arbitrary datum. For a fluid of weight (ρg) at a height y above the established datum, the potential energy is wy. Thus, the potential energy per unit weight of fluid can be expressed as simply the height above the datum,
Combining the energy terms for kinetic and potential energies along with influences due to pressure and headloss, results in the following equation:
Where: y = the vertical distance from the datum (length) P = pressure (weight/volume) hf = headloss due to friction (length)
As the fluid moves downstream, energy is lost due to friction. These losses can be due to channel bed roughness, channel constrictions, and other flow structures. Energy loss due to friction is neglected in this analysis.
Equation 4 evaluates the flow at two locations: point 1 (upstream) and point 2 (downstream). As mentioned previously, the pressure at locations 1 and 2 both equal atmospheric pressure in open-channel flow, therefore the pressure terms cancel out. Headloss due to friction is also neglected when determining specific energy; therefore this term disappears as well. After these cancelations, the equation becomes,
and the total specific energy at any point in the system is,
Volumetric discharge
To evaluate the kinetic-energy term, the fluid velocity is needed. The volumetric discharge, Q is typically used in open channel flow calculations. For rectangular channels, the unit discharge is also used, and many alternative formulas for rectangular channels use this term instead of v or Q. In US customary units, Q is in ft3/sec. and q is in ft2/sec.
Where: q = unit discharge (length2/time) Q = volumetric discharge (length3/time) b = base width of rectangular channel (length)
Equation 6 can then be rewritten for rectangular channels as,
The E–y diagram
For a given discharge, the specific energy can be calculated for various flow depths and plotted on an E–y diagram. A typical E–y diagram is shown below.
Three different q values are plotted on the specific energy diagram above. The unit discharges increase from left to right, meaning that q1 < q2 < q3. There is a distinct asymptotic relationship as the top part of the curve approaches the E = y line and the bottom part of the curve tends toward the x-axis. Also shown are the critical energy or minimum energy, Ec and the corresponding critical depth value, yc. The values shown are for the q1 discharge only, but unique critical values exist for any discharge.
Critical flow relationships
The critical depth value mentioned in the E–y diagram section above is mathematically represented by the ratio of the fluid velocity to the velocity of a small amplitude gravity wave. This ratio is called the Froude number.
The critical depth has a Froude number equal to one and corresponds to the minimum energy a flow can possess for a given discharge. Not all flows are critical, so what about Froude numbers not equal to one? Froude numbers below one are considered subcritical and Froude numbers above one are considered supercritical.
Physically, subcritical flow is deep and the velocities are slow. This means subcritical flow has high potential energy and low kinetic energy. Supercritical flow on the other hand tends to be shallow and the velocities are fast. Supercritical flow has low potential energy and high kinetic energy.
If we refer back to the E–y diagram, it is seen that a line passes through the critical value on each successive discharge curve. This line corresponds to .
Depth values on the E–y curve greater than the critical depth correspond to subcritical flow depths. Likewise, values less than the critical depth correspond to supercritical flow depths.
For rectangular channels, the critical depth can be calculated by taking the derivative of the energy equation and setting it equal to zero. The energy associated with the critical depth is found by placing the critical depth expression into the specific energy equation. The critical energy expression is demonstrated graphically by the line , which connects critical depth values.
Alternate depths
For a given energy value and discharge, there generally exists two possible corresponding flow depths. In the diagram above, the alternate depths are labeled y1 and y2 and correspond to the subcritical and supercritical flow regions, respectively. This holds true for all energy values greater than critical energy. This relationship does not hold true at critical energy where only the critical depth, yc, is possible and for energy values less than critical depth’s energy where there are no positive depths. The following equation can be used to solve for one alternate depth in terms of the other in rectangular channels. The values for y1 and y2 are interchangeable.
Theory and derivation of alternate depth relationship
In the open-channel flow of rectangular channels, the alternate depth equation relates the upstream(y1) and downstream(y2) steady-state flow depths of a flow that encounters a control device, such as a sluice gate, which conserves energy for a given discharge.
The alternate depth equation can be derived in a similar fashion as the conjugate depth equation. In the open-channel flow of rectangular channels, the conjugate depth equation relates the upstream(y1) and downstream(y2) steady-state flow depths for a flow that encounters a pure hydraulic jump, which conserves momentum for a given discharge. The mathematical derivation of the conjugate depth equation can be a useful tool in understanding the derivation of the alternate depth equation, please refer to the above link for a more in-depth discussion of its derivation.
Conjugate depth equation
Duality relationship between momentum and specific energy functions and the derivation of the alternate depth relationship
Another important concept that can be applied towards the derivation the alternate depth equation arises from the comparison of the dimensionless momentum function to the dimensionless specific energy function. It can be seen that the dimensionless momentum function (M') has the identical functional relationship as the dimensionless specific energy function (E") when both are properly transformed. (Henderson 1966). From this comparison it can be observed that any result that applies to the dimensionless momentum equation (M') would likewise apply to the dimensionless specific energy equation (E"). From this duality concept we can determine the analog to the conjugate depth equation for the specific energy equation to provide an analytical relationship between alternate depths y1 and y2. Below gives the mathematical derivations behind this concept:
Dimensionless momentum function
- 1) Starting with the momentum function for a rectangular channel:
- 2) Divide through by (yc2 ) to obtain dimensionless form:
Dimensionless specific-energy function
- 1) Starting with the specific-energy function for a rectangular channel:
- 2) Divide through by yc to obtain dimensionless form:
- 4) Setting and substituting into equation (22) we find the final dimensionless form of the specific-energy function:
Through the comparison of the dimensionless momentum and specific-energy functions it can be observed that our final dimensionless specific-energy equation is identical to the functional relationship as was determined for the dimensionless-momentum equation:
Therefore any result that applies to the dimensionless-momentum equation would likewise apply to the dimensionless specific-energy equation, provided the transform is used.
Derivation of alternate depth equation
Using the conjugate depth equation and the duality concept between the dimensionless forms of the momentum (M') and specific energy (E") functions an analytical relationship between alternate depths can be obtained.
- 1) Start with the conjugate depth equation (eq. 17):
- 2) Develop the analog to Fr1 by observing that the dimensionless momentum equation (eq. 20) has a value of y' equal to unity at critical depth. If we chose then the resulting M-y relationship will be numerically identical to the dimensionless M'-y' relationship since yc is unity. For this unit discharge q, the Froude number simplifies to:
- 3) Although dimensionally y1 and y1" are different, their numerical magnitudes are the same at unity and thus we can express the analog of the Fr1 in the conjugate depth equation as:
- where the tilde in the symbol indicates that this is simply the specific-energy equation analog to the Froude number in this analysis.
- 5) Observing that and , equation (26) can be simplified to the final analytical alternate depth relationship:
- 6) Recalling that for rectangular channels, and and recognizing that , the final analytical alternative depth relationship can also be represented as:
Notice that because of the symmetry of the original conjugate depth equation, the resulting dimensionless alternate depth equation applies regardless of the Froude number at location 1. That is, y1 may correspond to either supercritical or subcritical flow conditions. The alternate depth relationship will yield the alternate depth to y1 corresponding to the opposite flow regime in either case.
To the best of the author’s knowledge, this final result for the alternate depth relationship appears in no textbook and is an original contribution by Dr. Glenn E. Moglen of Virginia Tech and appears on this website through the assistance of Paul Le Bel and the CEE 5984 Open Channel Flow course at Virginia Tech.
Example
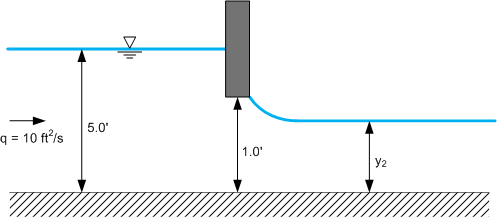
The concept of alternate depths can be demonstrated with a sluice gate example. Sluice gates are used to control the flow of water in open channels and under ideal conditions, where friction is ignored, they conserve energy for a given discharge.
Water flows in a rectangular channel that contains a sluice gate. The upstream depth of flow, y1 is 5.0 ft, the sluice gate opening is 1.0 ft, and the unit discharge is, . What is the flow depth downstream of the sluice gate, y2?
Since energy is conserved at a sluice gate, the upstream and downstream energies are equal, or . The specific energy equation (eq. 8), alternate depth equation (eq.16), and an E–y diagram are used to demonstrate how to solve this problem.
Compare specific energies at upstream(y1) and downstream(y2) depths to demonstrate conservation of energy () at a sluice gate:
Therefore and energy is conserved.
This topic contribution was made in partial fulfillment of the requirements for Virginia Tech, Department of Civil and Environmental Engineering course: CEE 5984 – Open Channel Flow during the Fall 2011 semester.
See also
References
- M. H. Chaudhry, Open-Channel Flow. New York: Springer, 2008.
- E. J. Finnemore and J.B. Franzini, Fluid Mechanics with Engineering Applications. New York: McGraw-Hill, 2002.
- Moglen, G.E. (2010) Lecture notes from CEE 4324/5984: Open Channel Flow, Virginia Tech <http://filebox.vt.edu/users/moglen/ocf/index.html>, September 2, 2010.
- Henderson, F.M., 1966. Open Channel Flow, Prentice-Hall.
- Moglen, Glenn E. Summary Table of Basic Open Channel Flow Relationships. Virginia Tech CEE 4324/5984 Open Channel Flow. PDF.