Radial set
Gear design is the process of designing a gear. Designing is done prior to manufacturing and includes calculation of the gear geometry, taking into account gear strength, wear characteristic of the gear teeth, material selection, gear alignment and provision for lubrication of gear.
Gear
A gear is a rotating machine part which has cut teeth, that mesh with another toothed part in order to transmit torque. The cut teeth are also called 'cogs'. Gears are one of the most important parts of any machine or a mechanism. Some of the sectors in which gears play a vital role are:
- Turbine plant
- Hot and Cold Rolling
- Construction machinery
- Elevator industry
Gear tooth terminology
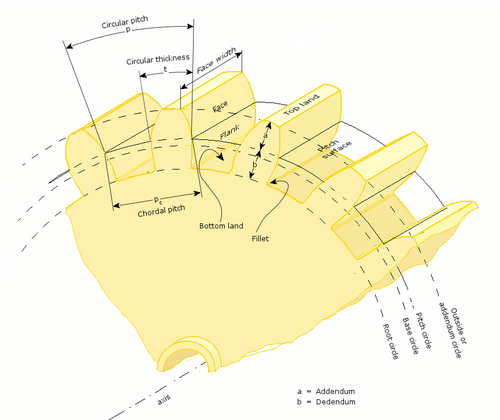
Standard system of Gear Teeth
In a gear drive, two types of curves, the cycloidal and the involute, are generally used. In a gear drive, the shape of the tooth depends upon the pressure angle. Gears of involute profile with 14.5°, 20° full-depth and 20° stub pressure angles are most commonly used in industries. A 20° pressure angle full-depth involute gear tooth has various advantages over the other pressure angles. BIS has recommended the use of 20° pressure angle full depth involute gear tooth.
Design Considerations[1]
The accuracy of the output of a gear depends on the accuracy of its design and manufacturing. The correct manufacturing of a gear requires a number of prerequisite calculations and design considerations. The design considerations taken into account before manufacturing of gears are:
- Strength of the gear in order to avoid failure at starting torques or under dynamic loading during running conditions.
- Gear teeth must have good wear characteristics.
- Selection of material combination.
- Proper alignment and compactness of drive
- Provision of adequate and proper lubrication arrangement.
Selection of Materials
The gear material should have the following properties:
- High tensile strength to prevent failure against static loads
- High endurance strength to withstand dynamic loads
- Low coefficient of friction
- Good manufacturability
Generally cast iron, steel, brass and bronze are preferred for manufacturing metallic gears with cut teeth. Where smooth action is not important, cast iron gears with cut teeth may be employed. Commercially cut gears have a pitch line velocity of about 5 metre/second. For velocities larger than this, gear sets with non-metallic pinions as one member are used to eliminate vibration and noise. Non-metallic materials are made of various materials such as treated cotton pressed and moulded at high-pressure, synthetic resins of the phenol type and rawhide. Moisture affects rawhide pinions. Gears made of phenolic resins are self-supporting on the other hand other two types are supported by metal side plates at both ends of the plate. Large wheels are made with fretting rings to save alloy steels. Wheel centre is commonly cast from cast iron. The ring is forged or roll expanded from steel of the respective grade specified by the tooth design.
Gear wheel proportions
A gear has three important parts
- Hub
- Web or arms
- Rim
Hub of gears are of two types, solid or split. The advantage of split hub is that it reduces the cooling stresses in the gear and facilitates the mounting of the gear on the shaft. The solid hub gear is to be mounted overhung on the shaft. The key is placed under the arm in case of solid hub while in case of split hub, the key is placed at right angles to the hub joint.
Small gears up to 250 mm pitch circle diameter are built with a web, which joins the hub and the rim. The thickness of the web of the gear should be such that it is capable of transmitting the torque without shearing off at the hub where it joins. The gear is designed such that the thickness of its web is equal to half the circular pitch. Gear of larger diameter are provided with arms. The number of arms depends on the pitch circle diameter of the gear. Following are the prevailing practices of the number of arms and gear diameters
| Gear diameter(mm) | Arms |
|---|---|
| 300-500 | 4-5 |
| 500-1500 | 6 |
| 1500-2400 | 8 |
| >2400 | 10-12 |
While calculating the dimensions of the arms it is assumed that they transmit the stalling torque safely. Elliptical cross sections are preferred for lighter loads while remaining cross sections are used for large and heavy gears. The following aspects are considered while determining cross sectional diameter of the arm.
Empirical formulas are used to determine the rim thickness.
where is the number of teeth and are the number of arms.
A good design is a one in which the rim has a central rib of thickness equal to half the circular pitch.
If the lay out of the shaft is known, the diameter of the gear shaft can be calculated. Toothed wheels fixed on the shaft are fitted by interference-for example, press or light press fit. For impact load or speeds above 2000 r.p.m. press fit is employed. If the wheel is to be removed from the shaft medium fit are used.
The following types of gears are most commonly used in industry for power transmission purposes:
- Spur gears
- Helical gears
- Bevel gears
- Worm and worm gears
=
- <
References
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534