Span (category theory)
In physics, invariance mechanics, in its simplest form, is the rewriting of the laws of quantum field theory in terms of invariant quantities only. For example, the positions of a set of particles in a particular coordinate system is not invariant under translations of the system. However, the (4-dimensional) distances between the particles is invariant under translations, rotations and Lorentz transformations of the system.
The invariant quantities made from the input and output states of a system are the only quantities needed to give a probability amplitude to a given system. This is what is meant by the system obeying a symmetry. Since all the quantities involved are relative quantities, invariance mechanics can be thought of as taking relativity theory to its natural limit.
Invariance mechanics has strong links with loop quantum gravity in which the invariant quantities are based on angular momentum. In invariance mechanics, space and time come secondary to the invariants and are seen as useful concepts that emerge only in the large scale limit.
Feynman rules
The Feynman rules of a quantum system can be rewritten in terms of invariant quantities (plus constants such as mass, charge, etc.) The invariant quantities depend on the type of particle, scalar, vector or spinor. The rules often involve geometric quantities such as the volumes of simplices formed from vertices of the Feynman graphs.
Scalar particles
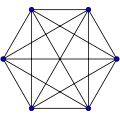
In a system of scalar particles, the only invariant quantities are the 4-dimensional distances (intervals) between the starting points () and ending points () of the particle paths. These points form a complete graph:
The invariants are the numbers
Vector particles
In a system of vector particles such as photons, the invariants are the 4-dimensional distances between the starting points and ending points of the particle paths, and the angles between the starting and ending polarisation vectors of the photons ( )
There are four invariants on each line:
Yang–Mills vector particles
Yang–Mills vector fields of a given gauge group also involve the angle representing a rotation of the gauge group ( ).
There are three invariants on each line:
Spinor fields
These involve the angles between the spinor vectors. The invariants are:
So for example, the fermion propagator is defined in relation to the massless scalar propagator as
Mixed systems
Systems usually consist of a mixture of scalar, spinor and vector fields and the invariants can depend on angles between spinors and vectors. To simplify this process ideas from twistor theory are often used which enables one to decompose a null-vector into a pair of spinors. Alternatively 3-point invariants can be introduced such as the spinor-spinor-vector triangle invariant:
It is important to note that some types of invariants are combinations of other types invariants, for example the angles in a complete-graph are invariants but they can be found as combinations of distance invariants.
In chromodynamics, for example, there are 4-point invariants also. So for a completely specified system you would have several numbers assigned to each line, triangle and tetrahedron in a complete graph representing the system.
One outstanding problem is that of enumerating all the possible invariants which can be made from the various spin and polarisation vectors.
Constraints
A system represented by a complete graph contains many invariant quantities. For large graphs, however, not all these quantities are independent and we must specify dimensional and gauge constraints. Why the particular number of dimensions or particular gauge group is chosen is still not known. The constraints and whether they are satisfied exactly or approximately is the key to invariance mechanics and the difference between it and conventional field theory. Work is being done to see whether the breaking of these constraints is a consequence of the gravitational field. If the constraints are satisfied only approximately, i.e. if there is a quantum uncertainty in the constraints then they are best thought of as local maxima of the amplitudes of a system which occur due to the specific Feynman rules used.
Dimensions
Since invariance mechanics does not explicitly use coordinate systems, the definition of dimension is slightly different. The equivalent way of expressing the number of dimensions is given, as in distance geometry, as specifying that the volume of any (D + 2)-simplex made from the points in the system is zero. The volume of a simplex is given by a formula involving the invariant distances (the R's) between the points which is given by the Cayley–Menger determinants. If this determinant is exactly 0 for all simplices then the geometry is Euclidean. If the determinant is only approximately 0 then at small distances space-time is non-Euclidean. This has deep connections with quantum foam and loop quantum gravity.
For Minkowski space, or for any space with signature (+ + + ... + − ) this makes no difference to the formulae for invariance mechanics.
Gravity
By allowing quantum uncertainty in the dimensional constraints (which involves replacing delta functions with reciprocal functions in the equations), the geometry is no longer confined to flat space-time, this break from flat space-time can be seen as a curvature and, just as in General Relativity can be seen as the cause of gravity. This is called 'off-dimension' physics in analogy to off-shell physics.
Gauge group
In a similar way to expressing the number of dimensions, the dimension and type of the gauge group is given by an identity involving the polarisation (or spin) invariants (the S, T and U's). In the simple cases such as for the photon, these are simply spherical versions of the Cayley–Menger determinants. The gauge group is an internal symmetry because the gauge identity involves far more quantities than the dimensional identity. A simple gauge group such as SU(5) or involves fewer invariants than a non-simple gauge group such as U(1)xSU(2)xSU(3) (see: Standard Model). There has been recent work on combining the dimensional and gauge constraints into a single equation to produce a unified theory. It is thought that this will be achieved by combining of the invariants on each line into a single complex number (or hypercomplex number).
Supersymmetry
In the supersymmetric model, some of the spinor invariants and vector invariants are combined together into a single invariant. Having fewer invariants means that there is more symmetry and more transformations are possible such as transformations between fermions and bosons. It is believed, although currently unproved, that the minimum number of invariants on each line of a complete graph representing a system is two – those being the 4-dimensional distances (the R's) and an angle representing the rotation from one particle 'flavour' to another particle 'flavour' (the T's). Some have suggested that even these invariants can be combined into one by saying that the 4 dimensions of space and time are just 4 more flavours that a particle can have, albeit ones which can change very little (compared with the size of the Universe as a whole). Models of this type imply that the universe has an overall spherical geometry. The mixing of space-time and flavour symmetries adds an additional degree of freedom to a particle's light-cone which appears as a unique mass for each particle depending on the flavour.
Having a small number of invariants doesn't necessarily make a simpler model since all the complexity of the model is bound up in the constraints which can be polynomials of hundreds of variables. One of the primary aims of invariance mechanics is to find these polynomial(s) and to find which symmetry group they correspond to. Many believe that the permutation of the variables of these polynomial(s) will correspond to one of the special sporadic groups. (Interestingly, only the largest sporadic group, the monster group is big enough to incorporate the constraints for the Standard Model). The other main aim is to find appropriate Feynman rules on the invariants which both accurately describe nature and don't lead to infinities.
M-theory
Although invariance mechanics was born out of trying to understand point particle theory, possible connections with superstring and M-theory have emerged. The argument is that the smallest simplex which needs a constraint to be 4-dimensional is the 6-simplex. This can be viewed as the endpoints of a 3-simplex (a triangular membrane) moving through time. The propagator function of this would be which is the inverse of the volume of a 6-simplex. In other words the greatest probability would be when the volume of this 6-simplex is 0 and hence it is embedded in 4 dimensions. Hence the propagator for a particle would the same as the dimensional constraint. So if the Universe is built out of 6 simplices then the dimensional constraint can be applied to all simplices. Other fields of work are investigating whether the distance invariants may take only discrete values and whether areas or volumes should be taken as the fundamental invariants. (The dual of loop quantum gravity involves quantized areas).
Others take the view that in invariance mechanics it should be irrelevant whether you view the fundamental constituents as particles or strings or membranes and a more formal approach is called for.
History
The history of invariance mechanics is difficult to pinpoint since many people have been working on it without realizing that they were working on invariance mechanics. Notable milestones include the 4-dimensional invariant found by Henri Poincaré in special relativity (1905), Yang–Mills gauge invariants theory. Roger Penrose and his spin-networks (1960's) influenced the subject. Cayley–Menger and their invariant based metric theory was an important milestone. Recently Baratin–Freidel (2006) have demonstrated the connection between invariance mechanics and loop quantum gravity.