Spiral antenna

Five-limit tuning, or 5-limit tuning is a method to obtain a justly tuned musical scale. The frequencies of the notes of such a scale are obtained by multiplying the frequency of a given reference note (the base note) by powers of 2, 3, or 5, or a combination of them. For instance, if the base note is C and its frequency is f_C, the frequency of E is

$f_{E}=5^{1}\cdot 2^{-2}\cdot f_{C}={5 \over 4}f_{C}$

In other words, the ratio between the two frequencies (interval ratio) is:

${f_{E} \over f_{C}}={5 \over 4}$

This implies that the tones defined by this system are regular number harmonics of a single fundamental frequency (possibly other than the tonic), as do Pythagorean and all just tunings.

Diatonic scale

It is possible to tune the familiar diatonic scale or chromatic scale in just intonation in many ways, all of which make certain chords purely tuned and as consonant and stable as possible, and the other chords not accommodated and considerably less stable.

The prominent notes of a given scale are tuned so that their frequencies form ratios of relatively small integers. For example, in the key of G major, the ratio of the frequencies of the notes G to D (a perfect fifth) is 3/2, while that of G to C (a perfect fourth) is 4/3. Three basic intervals can be used to construct any interval involving the prime numbers 2, 3, and 5 (known as 5-limit just intonation):

• s = 16:15 (Semitone)
• t = 10:9 (Minor tone)
• T = 9:8 (Major tone)

which combine to form:

• 6:5 = Ts (minor third)
• 5:4 = Tt (major third)
• 4:3 = Tts (perfect fourth)
• 3:2 = TTts (perfect fifth)
• 2:1 = TTTttss (octave)

Primary triads in C My name: Lindsey Gavin
My age: 28
Country: Sweden
Home town: Vemdalen
Postal code: 840 92
Address: Buanvagen 79

Look into my weblog :: http://www.hostgator1centcoupon.info/.

A just diatonic scale may be derived as follows. Suppose we insist that the chords CEG, FAC, and GBD be just major triads (with frequency ratios 4:5:6). As a consequence, we obtain a scale in which EGB and ACE and are just minor triads (10:12:15), but DFA (27:32:40) and BDF (45:54:64) are non-just minor triads:

Note	Name	C		D		E		F		G		A		B		C
	Ratio	1/1		9/8		5/4		4/3		3/2		5/3		15/8		2/1
	Natural	24		27		30		32		36		40		45		48
	Cents	0		204		386		498		702		884		1088		1200
Step	Name		T		t		s		T		t		T		s
	Ratio		9/8		10/9		16/15		9/8		10/9		9/8		16/15
	Cents		204		182		112		204		182		204		112

This is known as Ptolemy's intense diatonic scale. Here the row headed "Natural" expresses all these ratios using a common list of natural numbers (by multiplying the row above by the lcm of its denominators). The major thirds are correct; two minor thirds are right, but D to F is a semiditone or Pythagorean minor third (equal to three just perfect fifths, descending), a syntonic comma narrower than a justly tuned minor third.

Another way to do it is as follows. We can insist that the chords DFA, EGB, and ACE be just minor triads. Then FAC and CEG are just major triads, but GBD is a non-just major triad, and BDF is a non-just minor triad:

Note	A		B		C		D		E		F		G		A
Ratio	1/1		9/8		6/5		4/3		3/2		8/5		9/5		2/1
Natural	120		135		144		160		180		192		216		240
Cents	0		204		316		498		702		814		1018		1200
Step		T		s		t		T		s		T		t
Cent step		204		112		182		204		112		204		182

Again, the major thirds are correct; two minor thirds are right, but now B to D is not.

If we compare with the scale above, we see that six notes can be lined up, but one note, D, has changed its value. It is evidently not possible to get all seven chords mentioned correct.

There are other possibilities; instead of lowering D, we can raise A. But this breaks something else.

Twelve tone scale

To build a twelve tone scale in 5-limit tuning, we start by constructing a table containing fifteen justly intonated pitches:

Factor		1/9	1/3	1	3	9
5	note ratio cents	D− 10/9 182	A 5/3 884	E 5/4 386	B 15/8 1088	FTemplate:Music+ 45/32 590
1	note ratio cents	BTemplate:Music− 16/9 996	F 4/3 498	C 1 0	G 3/2 702	D 9/8 204
1/5	note ratio cents	GTemplate:Music− 64/45 610	DTemplate:Music− 16/15 112	ATemplate:Music 8/5 814	ETemplate:Music 6/5 316	BTemplate:Music 9/5 1018

The factors listed in the first row and column are powers of 3 and 5, respectively (e.g., 1/9 = 3⁻²). Colors indicate couples of enharmonic notes with almost identical pitch. The ratios are all expressed relative to C in the centre of this diagram (the base note for this scale). They are computed in two steps:

1. For each cell of the table, a base ratio is obtained by multiplying the corresponding factors. For instance, the base ratio for the lower-left cell is 1/9 · 1/5 = 1/45.
2. The base ratio is then multiplied by a negative or positive power of 2, as large as needed to bring it within the range of the octave starting from C (from 1/1 to 2/1). For instance, the base ratio for the lower left cell (1/45) is multiplied by 2⁵, and the resulting ratio is 64/45, which is a number between 1/1 and 2/1.

Note that the powers of 2 used in the second step may be interpreted as ascending or descending octaves. For instance, multiplying the frequency of a note by 2⁵ means increasing it by 5 octaves. Moreover, each row of the table may be considered to be a sequence of fifths (ascending to the right), and each column a sequence of major thirds (ascending upward). For instance, in the first row of the table, there is an ascending fifth from D and A, and another one (followed by a descending octave) from A to E. This suggests an alternative but equivalent method for computing the same ratios. For instance, you can obtain A (5/3 ratio), starting from C, by moving one cell to the left and one upward in the table, which means descending by one fifth (2/3) and ascending by one major third (5/4):

${1 \over 1}\cdot {2 \over 3}\cdot {5 \over 4}={10 \over 12}={5 \over 6}.$

Since this is below C, you need to move up by an octave to end up within the desired range of ratios (from 1/1 to 2/1):

${5 \over 6}\cdot {2 \over 1}={10 \over 6}={5 \over 3}.$

A 12 tone scale is obtained by removing one note for each couple of enharmonic notes. This can be done in at least three ways, which have in common the removal of GTemplate:Music, according to a convention which was valid even for C-based Pythagorean and 1/4-comma meantone scales. The first strategy, which we operationally denote here as symmetric scale 1, consists of selecting for removal the tones in the upper left and lower right corners of the table. The second one, denoted as symmetric scale 2, consists of discarding the notes in the first and last cell of the second row (labeled "1"). The third one, denoted as asymmetric scale, consists of discarding the first column (labeled "1/9"). The resulting 12-tone scales are shown below:

48 year-old Registered Nurse (Medical ) Rave from Pickering, enjoys to spend time individuals watching, new property for sale developers in singapore and cave diving. Finished a cruise liner experience that included passing by Chan Chan Archaeological Zone.

Symmetric scale 1
Factor	1/9	1/3	1	3	9
5		A 5/3	E 5/4	B 15/8	FTemplate:Music+ 45/32
1	BTemplate:Music− 16/9	F 4/3	C 1	G 3/2	D 9/8
1/5		DTemplate:Music− 16/15	ATemplate:Music 8/5	ETemplate:Music 6/5

40 year old Supply and Circulation Manager Courtney from Aberdeen, has several pursuits including bmx, property developers in new project launch singapore and actions. Finds travel a wonderful experience after visiting Central Sikhote-Alin.

Symmetric scale 2
Factor	1/9	1/3	1	3	9
5	D− 10/9	A 5/3	E 5/4	B 15/8	FTemplate:Music+ 45/32
1		F 4/3	C 1	G 3/2
1/5		DTemplate:Music− 16/15	ATemplate:Music 8/5	ETemplate:Music 6/5	BTemplate:Music 9/5

40 year old Supply and Circulation Manager Courtney from Aberdeen, has several pursuits including bmx, property developers in new project launch singapore and actions. Finds travel a wonderful experience after visiting Central Sikhote-Alin.

Asymmetric scale
Factor	1/9	1/3	1	3	9
5		A 5/3	E 5/4	B 15/8	FTemplate:Music+ 45/32
1		F 4/3	C 1	G 3/2	D 9/8
1/5		DTemplate:Music− 16/15	ATemplate:Music 8/5	ETemplate:Music 6/5	BTemplate:Music 9/5

Trying to invest in Singapore Actual Property , or are you attempting to promote, hire, invest, buy buy a Singapore property ? Properly then, you may have come to the fitting place in your seek for Singapore properties. Here, we are going to aid you find your dream Singapore property from our market itemizing of 1000's of Singapore properties in our Singapore real property database.

Overseas particular person who want to buy/ purchase a Restricted residential property in Sentosa Cove can acquire fast observe approval from Singapore Land Dealing Unit. Overseas particular person who want to purchase/ acquire a Restricted residential property in Sentosa Cove can apply for a long term social visit move underneath this Scheme to facilitate entry into Singapore. Foreign individual who want to apply for permanent residency in Singapore can contact SLA or MAS permitted institutions. The place you're shopping for property which is below development, the Singapore Academyof Regulation will maintain a portion of the acquisition monies as stakeholders till the expiryof the defects legal responsibility interval supplied in the Agreement/Contract. D19) Hougang / Punggol / Sengkang Condominium Common Room with Aircon

A international individual (any one who isn't a Singapore citizen, Singapore Company, Singapore restricted liability partnership or a Singapore society) will still want approval from the Singapore Land Authority (SLA) to purchase land-titled property such as houses, bungalows and vacant plots of land. Housing Improvement Board Properties SINGAPORE NON-PUBLIC RESIDENTIAL PROPERTIES Singapore firm; Singapore society. We provide invaluable services to expats who are considering relocation to Singapore For every kind of Singapore property related providers, we're there to obtain your name. You are positive to get one of the best Singapore properties with our help. RE/MAX Singapore Singapore Residential Business and Industrial Singapore citizen; Singapore Land Authority Thomson Highway, Singapore

Nevertheless, additionally it is a foul investment decision to go in too early. For instance you buy a property near one of the new MRT station location at the Thomson line. Because it takes 10 years to be accomplished, you might need difficulties renting that place out to pay off your mortgage payments. In addition, 10 years is a long time when something can occur including recession, new properties being introduced, modifications in interest rates etc. All these can have an adversarial impact on your property funding.

First, there are generally more rental transactions than gross sales transactions, to permit AV to be determined for every property based on comparable properties. Second, actions in sale costs are extra unstable than rentals. Therefore, using rental transactions to derive the AV helps to maintain property tax extra steady for property owners. If you are shopping for or trying to hire a property. It's tiring to call up individual property agent, prepare appointments, coordinate timing and to go for individual property viewing. What most individuals do is to have a property agent representing them who will organize and coordinate the viewings for all of the properties out there based mostly in your requirements & most well-liked timing. Rent Property District 12 Lease Property District thirteen

The brokers say that many Chinese language patrons are also investing abroad so they can personal property close to major instructional establishments. Some are buying houses close to top faculties — despite the fact that their youngsters are so little they can not walk but. Greater than 80 % of rich Chinese need to ship their children overseas to school, based on the Hurun Report, a Shanghai-based mostly publication. Chinese language patrons sometimes used to pick up properties within the $1 to $5 million vary in New York, typically shopping for two and three at a time for funding purposes, the brokers mentioned. Monika Tu, a dealer at high-end real estate agency Black Diamondz Property Concierge in Sydney, says that over the previous yr mainland Chinese language have develop into 80 % of her firm's business. WCEGA Plaza & Tower

An insurance coverage that covers the reinstatement worth or outstanding loan, whichever is decrease, within the event that the property search singapore (view site…) it insures is destroyed by fire. The coverage does not embody dwelling renovations, moveable household contents and personal belongings. Mortgage Insurance Credit bureau checks (e.g., Good payment data for bank cards / previous or existing loans, no previous blemishes corresponding to discharged bankrupts) A sign by the financial institution of the quantity of mortgage that you are eligible for. Nonetheless, an AIP doesn't constitute a binding loan offer. Additional checks and situations may be imposed by the financial institution, and the phrases of the formal supply will even rely upon the property that you simply intend to buy. Freehold / leasehold (999 years / 99 years)

In the first and second scale, BTemplate:Music and D are exactly the inversion of each other. This is not true for the third one. This is the reason why these two scales are regarded as symmetric (although the removal of GTemplate:Music makes all 12 tone scales, including those produced with any other tuning system, slightly asymmetric).

The asymmetric system has the advantage of having the "justest" ratios (those containing smaller numbers), nine pure fifths (factor 3/2), eight pure major thirds (factor 5/4) by design, but also six pure minor thirds (factor 6/5). However, it also contains two impure fifths (e.g. D to A is 40/27 rather than 3/2) and three impure minor thirds (e.g. D to F is 32/27 rather than 6/5), which practically limits modulation to a narrow range of keys. The chords of the tonic C, dominant G and subdominant F are pure, as well as DTemplate:Music, ATemplate:Music, ETemplate:Music and the minor chords Fm, Cm, Gm, Am, Bm and Em, but not the Dm.

A drawback of the asymmetric system is that it produces 14 wolf intervals, rather than 12 as for the symmetric ones (see below).

The BTemplate:Music in the first symmetric scale differs from the BTemplate:Music in the other scales by the syntonic comma, being over 21 cents. In equally tempered scales, the difference is eliminated by making all steps the same frequency ratio.

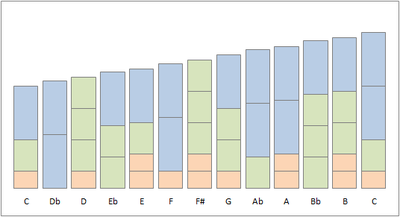Asymmetric scale built by stacking frequency factors 2/1 (blue), 3/2 (green), and 5/4 (brown) on a logarithmic scale

The construction of the asymmetric scale is graphically shown in the picture. Each block has the height in cents of the constructive frequency ratios 2/1, 3/2 and 5/4. Recurring patterns can be recognised. For example, many times the next note is created by replacing a 5/4-block and a 3/2-block by a 2/1-block, or a ratio of 16/15.

For a similar image, built using frequency factors 2, 3, and 5, rather than 2/1, 3/2, and 5/4, see here.

The justest ratios

The just ratios used to build these scales can be used as a reference to evaluate the consonance of intervals in other scales (for instance, see this comparison table). However, 5-limit tuning is not the only method to obtain just intonation. It is possible to construct just intervals with even "juster" ratios, or alternately, with values closer to the equal-tempered equivalents. For instance, a 7-limit tuning is sometimes used to obtain a slightly juster and consequently more consonant interval for the minor seventh (7/4) and its inversion, the major second (8/7). A list of these reference ratios, which may be referred to as pure or strictly just intervals or ratios, is provided below:

Interval name	Short	Number of semitones	5-limit tuning				7-limit tuning	17-limit tuning
			Symmetric scales		Asymmetric scales
			N. 1	N. 2	Standard	Extended
Perfect unison	P1	0	1/1	1/1	1/1	1/1	1/1	1/1
Minor second	m2	1	16/15	16/15	16/15	16/15	16/15	16/15
Major second	M2	2	9/8	10/9	9/8	9/8	8/7	8/7
Minor third	m3	3	6/5	6/5	6/5	6/5	6/5	6/5
Major third	M3	4	5/4	5/4	5/4	5/4	5/4	5/4
Perfect fourth	P4	5	4/3	4/3	4/3	4/3	4/3	4/3
Augmented fourth	A4	6	45/32	45/32	45/32	25/18	7/5	7/5 or 17/12
Diminished fifth	d5	6	64/45	64/45	64/45	36/25	10/7	10/7 or 24/17
Perfect fifth	P5	7	3/2	3/2	3/2	3/2	3/2	3/2
Minor sixth	m6	8	8/5	8/5	8/5	8/5	8/5	8/5
Major sixth	M6	9	5/3	5/3	5/3	5/3	5/3	5/3
Minor seventh	m7	10	16/9	9/5	9/5	9/5	7/4	7/4
Major seventh	M7	11	15/8	15/8	15/8	15/8	15/8	15/8
Perfect octave	P8	12	2/1	2/1	2/1	2/1	2/1	2/1

Cells highlighted in yellow indicate intervals that are juster than those in the non-coloured cells in the same row. Those highlighted in cyan indicate even juster ratios. The symmetric scale 2 has not been shown because it is a solution equivalent to the symmetric scale 1 (with respect to which has one juster and one less just interval) and is not frequently used for comparisons.

Notice that the ratios 45/32 and 64/45 for the tritones (augmented fourth and diminished fifth) are not in all contexts regarded as strictly just, but they are the justest possible in the above mentioned 5-limit tuning scales. An extended asymmetric 5-limit scale (see below) provides slightly juster ratios for both the tritones (25/18 and 36/25), the purity of which is also controversial. 7-limit tuning allows for the justest possible ratios, namely 7/5 (about 582.512 cents, also known as septimal tritone) and 10/7 (about 617.488 cents). These ratios are more consonant than 17/12 (about 603.000 cents) and 24/17 (about 597.000 cents), which can be obtained in 17-limit tuning, yet the latter are also fairly common, as they are closer to the equal-tempered value of 600.000 cents.

The above mentioned 7/4 interval (about 968.826 cents), also known as the septimal minor seventh, or harmonic seventh, has been a contentious issue throughout the history of music theory; it is 31 cents flatter than an equal-tempered minor seventh. SomeTemplate:Who assert the 7/4 is one of the blue notes used in jazz.

Size of intervals

The tables above show only the frequency ratios of each tone with respect to the base note C. However, intervals can be formed by starting from each of the twelve notes. Thus, twelve intervals can be defined for each interval type (twelve unisons, twelve semitones, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).

Frequency ratio of the 144 intervals in 12-tone 5-limit tuning (asymmetric scale; for symmetric scale 1, see here). Interval names are given in their standard shortened form. Pure intervals (as defined above) are shown in bold font.

Approximate size in cents of the 144 intervals in 12-tone 5-limit tuning (asymmetric scale; for symmetric scale 1, see here). Interval names are given in their standard shortened form. Pure intervals (as defined above) are shown in bold font.

In 5-limit tuning, each of the interval types, except for the unisons and the octaves, has three or even four different sizes. This is the price paid for seeking just intonation. The tables on the right and below show their frequency ratios and their approximate sizes in cents, for the "asymmetric scale". Similar tables, for the "symmetric scale 1", are published here and here. Interval names are given in their standard shortened form. For instance, the size of the interval from C to G, which is a perfect fifth (P5), can be found in the seventh column of the row labeled C. Pure intervals, as defined above, are shown in bold font (notice that, as explained above, the justly intonated ratio 45/32 ≈ 590 cents, for A4, is not considered to be pure).

A color code is used to distinguish the intervals which deviate from the reference sizes shown in the construction table, and to show the amount of their deviation. Wolf intervals are marked in black.

The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, the frequencies defined by construction for the twelve notes determine four different semitones (i.e. intervals between adjacent notes). For instance:

• $S_{1}={{5 \over 4}\div {6 \over 5}}={25 \over 24}\approx 70.672\ {\hbox{cents}}$
  ("Just" augmented unison between ETemplate:Music and E)
• $S_{2}={{9 \over 8}\div {16 \over 15}}={135 \over 128}\approx 92.179\ {\hbox{cents}}$
  (Augmented unison between DTemplate:Music and D)
• $S_{3}={16 \over 15}\approx 111.731\ {\hbox{cents}}$
  ("Just" minor second between C and DTemplate:Music)
• $S_{4}={{9 \over 5}\div {5 \over 3}}={27 \over 25}\approx 133.238\ {\hbox{cents}}$
  (Minor second between A and BTemplate:Music)

Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly

• $S_{E}={\sqrt[{12}]{2}}=100.000\ {\hbox{cents}}.$

As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.

Note that 5-limit tuning was designed to maximize the number of pure intervals, but even in this system several intervals are markedly impure (for instance, as shown in the figures, 60 out of 144 intervals deviate by at least 19.6 cents from the justly intonated reference sizes shown in the construction table). Also, 5-limit tuning yields a much larger number of wolf intervals with respect to Pythagorean tuning, which can be considered a 3-limit just intonation tuning. Namely, while Pythagorean tuning determines only 2 wolf intervals (a fifth and a fourth), the 5-limit symmetric scales produce 12 of them, and the asymmetric scale 14. It is also important to note that the two fifths, three minor thirds, and three major sixths marked in orange in the tables (ratio 40/27, 32/27, and 27/16 (or G−, ETemplate:Music−, and A+), even though they do not completely meet the conditions to be regarded as wolf intervals, deviate from the corresponding pure ratio by an amount (1 syntonic comma, i.e. 81/80, or about 21.5 cents) large enough to be clearly perceived as dissonant.

Clearly, the more we try to increase the number of pure and consonant intervals, the more the remaining ones become impure and dissonant, by compensation. Some of the major seconds (M2) and minor sevenths (m7) represent the only exception to this rule. As you can see in the tables, those marked in orange are pure (10/9 and 16/9), even if their size is 81/80 narrower than the corresponding reference size (9/8 and 9/5).

For a comparison with other tuning systems, see also this table.

Commas

In other tuning systems, a comma may be defined as a minute interval, equal to the difference between two kinds of semitones (diatonic and chromatic, also known as minor second, m2, or augmented unison, A1). In this case, however, 4 different kinds of semitones are produced (two A1, S₁ and S₂, and two m2, S₃ and S₄), and 12 different commas can be defined as the differences between their sizes in cents, or equivalently as the ratios between their ratios. Among these, we select the six ascending ones (those with ratio larger than 1/1, and positive size in cents):

Name of comma	Equivalent definitions		Size
	In meantone temperament	In 5-limit tuning (asymmetric scale)	Ratio	Cents
Diaschisma (DS)	${m2 \over A1}$ in 1/6-comma meantone	${S_{3} \over S_{2}}={{16 \over 15}\div {135 \over 128}}$	${2048 \over 2025}$	$19.6~$
Syntonic comma (SC)	${{LD} \over {DS}}={{GD} \over {LD}}$	${S_{2} \over S_{1}}={{135 \over 128}\div {25 \over 24}}$	${81 \over 80}$	$21.5~$
		${S_{4} \over S_{3}}={{27 \over 25}\div {16 \over 15}}$
Lesser diesis (LD)	${m2 \over A1}$ in 1/4-comma meantone	${S_{3} \over S_{1}}={{16 \over 15}\div {25 \over 24}}$	${128 \over 125}$	$41.1~$
		${S_{4} \over S_{2}}={{27 \over 25}\div {135 \over 128}}$
Greater diesis (GD)	${m2 \over A1}$ in 1/3-comma meantone	${S_{4} \over S_{1}}={{27 \over 25}\div {25 \over 24}}$	${648 \over 625}$	$62.6~$

The other six ratios are discarded because they are just the opposite of these, and hence they have exactly the same length, but an opposite direction (i.e. a descending direction, a ratio smaller than 1/1, and a negative size in cents). We obtain commas of four different sizes: the diaschisma, the lesser diesis, the syntonic comma, and the greater diesis. Since S₁ (the just A1) and S₃ (the just m2) are the most often occurring semitones in this 12-tone scale (see tables above), the lesser diesis, being defined as the ratio between them, is the most often observed comma.

The syntonic comma is also defined, in 5-limit tuning, as the ratio between the major tone (M2 with size 9/8) and the minor tone (M2 with size 10/9). Notice that it cannot be defined, in other tuning systems, as the ratio between diatonic and cromatic semitones (m2/A1), but it is an important reference value used to tune the perfect fifth in any tuning system in the syntonic temperament continuum (including also meantone temperaments).

Diminished seconds

Three of the above mentioned commas, namely the diaschisma, the diesis and the greater diesis, meet the definition of the diminished second, being the difference between the sizes in cents of a diatonic and a chromatic semitone (or equivalently the ratio between their frequency ratios).

On the contrary, the syntonic comma is defined either as the difference in cents between two chromatic semitones (S₂ and S₁), or between two diatonic semitones (S₄ and S₃), and cannot be considered to be a diminished second.

Extension of the twelve-tone scale

The table above uses only low powers of 3 and 5 to build the base ratios. However, it can be easily extended by using higher positive and negative powers of the same numbers, such as 5² = 25, 5⁻² = 1/25, 3³ = 27, or 3⁻³ = 1/27. A scale with 25, 35, or even more pitches can be obtained by combining these base ratios.

For instance, one can obtain 35 pitches by adding rows in each direction like this:

Factor		1/9	1/3	1	3	9
125	note ratio cents	ATemplate:Music 125/72 955.0	ETemplate:Music 125/96 457.0	BTemplate:Music 125/64 1158.9	FTemplate:Music+ 375/256 660.9	CTemplate:Music+ 1125/1024 162.9
25	note ratio cents	FTemplate:Music 25/18 568.7	CTemplate:Music 25/24 70.7	GTemplate:Music 25/16 772.6	DTemplate:Music 75/64 274.6	ATemplate:Music+ 225/128 976.5
5	note ratio cents	D− 10/9 182.4	A 5/3 884.4	E 5/4 386.3	B 15/8 1088.3	FTemplate:Music+ 45/32 590.2
1	note ratio cents	BTemplate:Music− 16/9 996.1	F 4/3 498.0	C 1/1 0.0	G 3/2 702.0	D 9/8 203.9
1/5	note ratio cents	GTemplate:Music− 64/45 609.8	DTemplate:Music− 16/15 111.7	ATemplate:Music 8/5 813.7	ETemplate:Music 6/5 315.6	BTemplate:Music 9/5 1017.6
1/25	note ratio cents	ETemplate:Music− 256/225 223.5	BTemplate:Music− 128/75 925.4	FTemplate:Music 32/25 427.4	CTemplate:Music 48/25 1129.3	GTemplate:Music 36/25 631.3
1/125	note ratio cents	CTemplate:Music− 2048/1125 1037.1	GTemplate:Music− 512/375 539.1	DTemplate:Music− 128/125 41.1	ATemplate:Music 192/125 743.0	ETemplate:Music 144/125 245.0

The left column (1/9) is sometimes removed (as in the asymmetric scale shown above), thus creating an asymmetric table with a smaller number of pitches. Notice that a juster ratio is produced for the diminished fifth (C-GTemplate:Music = 36/25), with respect to the restricted 5-limit tuning described above (where C to GTemplate:Music- = 64/45).

History

In Pythagorean tuning, perhaps the first tuning system to be theorized in the West, the only highly consonant intervals were the perfect fifth and its inversion, the perfect fourth. The Pythagorean major third (81:64) and minor third (32:27) were dissonant, and this prevented musicians from using triads and chords, forcing them for centuries to write music with relatively simple texture. In late Middle Ages, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant. For instance, if you decrease by a syntonic comma (81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated ratio of

${81 \over 64}\cdot {80 \over 81}={{1\cdot 5} \over {4\cdot 1}}={5 \over 4}$

and at the same time E-G is sharpened to the just ratio of

${32 \over 27}\cdot {81 \over 80}={{2\cdot 3} \over {1\cdot 5}}={6 \over 5}$

The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major triad (C-E-G).

By generalizing this simple rationale, Gioseffo Zarlino, in the late sixteenth century, created the first justly intonated 7-tone (diatonic) scale, which contained pure perfect fifths (3:2), pure major thirds, and pure minor thirds:

F → A → C → E → G → B → D

This is a sequence of just major thirds (M3, ratio 5:4) and just minor thirds (m3, ratio 6:5), starting from F:

F + M3 + m3 + M3 + m3 + M3 + m3

Since M3 + m3 = P5 (perfect fifth), i.e. 5/4 * 6/5 = 3/2, this is exactly equivalent to the diatonic scale obtained in 5-limit just intonation, and hence can be viewed as a subset of the construction table used for the 12-tone (chromatic) scale:

A	→	E	→	B
↑		↑		↑
F	→	C	→	G	→	D

where both rows are sequences of just fifths, and F-A, C-E, G-B are just major thirds:

M3		M3		M3
+		+		+
F	+	P5	+	P5	+	P5

See also

• Mathematics of musical scales
• Microtonal music
• Microtuner
• Pythagorean interval
• Semitone
• List of intervals in 5-limit just intonation
• List of meantone intervals
• List of musical intervals
• Whole-tone scale
• Regular number
• Hexany
• Electronic tuner
• Consonance and dissonance

Notes

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

External links

• Art of the States: microtonal/just intonation works using just intonation by American composers
• The Chrysalis Foundation -- Just Intonation: Two Definitions
• Dante Rosati's 21 Tone Just Intonation guitar
• Just Intonation by Mark Nowitzky
• Just Intonation Explained by Kyle Gann
• A selection of Just Intonation works edited by the Just Intonation Network web published on the Tellus Audio Cassette Magazine project archive at Ubuweb
• Medieval Music and Arts Foundation
• Music Novatory - Just Intonation
• Why does Just Intonation sound so good?
• The Wilson Archives
• Barbieri, Patrizio. Enharmonic instruments and music, 1470-1900. (2008) Latina, Il Levante
• 22 Note Just Intonation Keyboard Software with 12 Indian Instrument Sounds Libreria Editrice
• Plainsound Music Edition - JI music and research, information about the Helmholtz-Ellis JI Pitch Notation