Sersic profile
In physics and engineering, the time constant, usually denoted by the Greek letter (tau), is the parameter characterizing the response to a step input of a first-order, linear time-invariant (LTI) system.[1][note 1] The time constant is the main characteristic unit of a first-order LTI (linear time-invariant) system.
In the time domain, the usual choice to explore the time response is through the step response to a step input, or the impulse response to a Dirac delta function input.[2] In the frequency domain (for example, looking at the Fourier transform of the step response, or using an input that is a simple sinusoidal function of time) the time constant also determines the bandwidth of a first-order time-invariant system, that is, the frequency at which the output signal power drops to half the value it has at low frequencies.
The time constant also is used to characterize the frequency response of various signal processing systems – magnetic tapes, radio transmitters and receivers, record cutting and replay equipment, and digital filters – which can be modeled or approximated by first-order LTI systems. Other examples include time constant used in control systems for integral and derivative action controllers, which are often pneumatic, rather than electrical.
Time constants are a feature of the lumped system analysis (lumped capacity analysis method) for thermal systems, used when objects cool or warm uniformly under the influence of convective cooling or warming.[3]
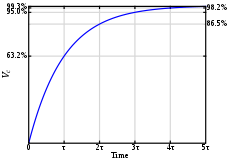
Physically, the constant represents the time it takes the system's step response to reach of its final (asymptotic) value. In radioactive decay the time constant is called the decay constant (λ), and it represents both the mean lifetime of a decaying system (such as an atom) before it decays, or the time it takes for all but 36.8% of the atoms to decay. For this reason, the time constant is longer than the half-life, which is the time for only 50% of the atoms to decay.
Differential equation
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. First order LTI systems are characterized by the differential equation
where τ represents the exponential decay constant and V is a function of time t
The right-hand side is the forcing function f(t) describing an external driving function of time, which can be regarded as the system input, to which V(t) is the response, or system output. Classical examples for f(t) are:
The Heaviside step function, often denoted by u(t):
the impulse function, often denoted by δ(t), and also the sinusoidal input function:
or
where A is the amplitude of the forcing function, f is the frequency in Hertz, and ω = 2π f is the frequency in radians per second.
Example solution
An example solution to the differential equation with initial value V0 and no forcing function is
where
is the initial value of V. Thus, the response is an exponential decay with time constant τ.
Discussion
Suppose
This behavior is referred to as a "decaying" exponential function. The time (tau) is referred to as the "time constant" and can be used (as in this case) to indicate how rapidly an exponential function decays.
Here:
Specific cases
After a period of one time constant the function reaches e−1 = approximately 37% of its initial value. In case 4, after five time constants the function reaches a value less than 1% of its original. In most cases this 1% threshold is considered sufficient to assume that the function has decayed to zero - as a rule of thumb, in control engineering a stable system is one that exhibits such an overall damped behavior.
Relation of time constant to bandwidth


Suppose the forcing function is chosen as sinusoidal so:
(Response to a real cosine or sine wave input can be obtained by taking the real or imaginary part of the final result by virtue of Euler's formula.) The general solution to this equation for times t ≥ 0 s, assuming V(t=0) = V0 is:
For long times the decaying exponentials become negligible and the so-called steady-state solution or long-time solution is:
The magnitude of this response is:
By convention, the bandwidth of this system is the frequency where |V∞|2 drops to half-value, or where ωτ = 1. This is the usual bandwidth convention, defined as the frequency range where power drops by less than half (at most −3 dB). Using the frequency in hertz, rather than radians/s (ω = 2πf):
The notation f3dB stems from the expression of power in decibels and the observation that half-power corresponds to a drop in the value of |V∞| by a factor of 1/√2 or by 3 decibels.
Thus, the time constant determines the bandwidth of this system.
Step response with arbitrary initial conditions

Suppose the forcing function is chosen as a step input so:
with u(t) the Heaviside step function. The general solution to this equation for times t ≥ 0 s, assuming V(t=0) = V0 is:
(It may be observed that this response is the ω → 0 limit of the above response to a sinusoidal input.)
The long-time solution is time independent and independent of initial conditions:
The time constant remains the same for the same system regardless of the starting conditions. Simply stated, a system approaches its final, steady-state situation at a constant rate, regardless of how close it is to that value at any arbitrary starting point.
For example, consider an electric motor whose startup is well modeled by a first-order LTI system. Suppose that when started from rest, the motor takes ⅛ of a second to reach 63% of its nominal speed of 100 RPM, or 63 RPM—a shortfall of 37 RPM. Then it will be found that after the next ⅛ of a second, the motor has sped up an additional 23 RPM, which equals 63% of that 37 RPM difference. This brings it to 86 RPM—still 14 RPM low. After a third ⅛ of a second, the motor will have gained an additional 9 RPM (63% of that 14 RPM difference), putting it at 95 RPM.
In fact, given any initial speed s ≤ 100 RPM, ⅛ of a second later this particular motor will have gained an additional 0.63 × (100 − s) RPM.
Examples of time constants
Time constants in electrical circuits

In an RL circuit composed of a single resistor and inductor, the time constant (in seconds) is
where R is the resistance (in ohms) and L is the inductance (in henries).
Similarly, in an RC circuit composed of a single resistor and capacitor, the time constant (in seconds) is:
where R is the resistance (in ohms) and C is the capacitance (in farads).
Electrical circuits are often more complex than these examples, and may exhibit multiple time constants (See Step response and Pole splitting for some examples.) In the case where feedback is present, a system may exhibit unstable, increasing oscillations. In addition, physical electrical circuits are seldom truly linear systems except for very low amplitude excitations; however, the approximation of linearity is widely used.
In digital electronic circuits another measure, the FO4 is often used. This can be converted to time constant units via the equation .[4]
Thermal time constant
Time constants are a feature of the lumped system analysis (lumped capacity analysis method) for thermal systems, used when objects cool or warm uniformly under the influence of convective cooling or warming. In this case, the heat transfer from the body to the ambient at a given time is proportional to the temperature difference between the body and the ambient:[5]
where h is heat transfer coefficient, and As is the surface area, T(t) = body temperature at time t, and Ta is the constant ambient temperature. The positive sign indicates the convention that F is positive when heat is leaving the body because its temperature is higher than the ambient temperature (F is an outward flux). If heat is lost to the ambient, this heat transfer leads to a drop in temperature of the body given by:[5]
where ρ = density, cp = specific heat and V is the body volume. The negative sign indicates the temperature drops when the heat transfer is outward from the body (that is, when F > 0). Equating these two expressions for the heat transfer,
Evidently, this is a first-order LTI system that can be cast in the form:
with
In other words, the time constant says that larger masses ρV and larger heat capacities cp lead to slower changes in temperature, while larger surface areas As and better heat transfer h lead to faster temperature changes.
Comparison with the introductory differential equation suggests the possible generalization to time-varying ambient temperatures Ta. However, retaining the simple constant ambient example, by substituting the variable ΔT ≡ (T − Ta), one finds:
Systems for which cooling satisfies the above exponential equation are said to satisfy Newton's law of cooling. The solution to this equation suggests that, in such systems, the difference between the temperature of the system and its surroundings ΔT as a function of time t, is given by:
where ΔT0 is the initial temperature difference, at time t= 0. In words, the body assumes the same temperature as the ambient at an exponentially slow rate determined by the time constant.
Time constants in neuroscience
In an action potential (or even in a passive spread of signal) in a neuron, the time constant is
where rm is the resistance across the membrane and cm is the capacitance of the membrane.
The resistance across the membrane is a function of the number of open ion channels and the capacitance is a function of the properties of the lipid bilayer.
The time constant is used to describe the rise and fall of membrane voltage, where the rise is described by
and the fall is described by
where voltage is in millivolts, time is in seconds, and is in seconds.
Vmax is defined as the maximum voltage attained in the action potential, where
where rm is the resistance across the membrane and I is the current.
Setting for t = for the rise sets V(t) equal to 0.63Vmax. This means that the time constant is the time elapsed after 63% of Vmax has been reached
Setting for t = for the fall sets V(t) equal to 0.37Vmax, meaning that the time constant is the time elapsed after it has fallen to 37% of Vmax.
The larger a time constant is, the slower the rise or fall of the potential of neuron. A long time constant can result in temporal summation, or the algebraic summation of repeated potentials.
Exponential decay
Template:See In exponential decay, such as of a radioactive isotope, the time constant can be interpreted as the mean lifetime. The half-life THL is related to the exponential time constant by
The reciprocal of the time constant is called the decay constant, and is denoted
Meteorological sensors
A time constant is the amount of time it takes for a meteorological sensor to respond to a rapid change in a measurand until it is measuring values within the accuracy tolerance usually expected of the sensor.
This most often applies to measurements of temperature, dewpoint temperature, humidity and air pressure. Radiosondes are especially affected due to their rapid increase in altitude.
See also
- RC time constant
- Cutoff frequency
- Exponential decay
- Length constant
- Rise time
- Fall time
- Frequency response
- Impulse response
- Step response
- Transition time
- Settling time
Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
External links
- Conversion of time constant τ to cutoff frequency fc and vice versa
- All about circuits - Voltage and current calculations
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1292037
- ↑ 5.0 5.1
20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
Cite error: <ref> tags exist for a group named "note", but no corresponding <references group="note"/> tag was found












































