Regular prime

Name: Jodi Junker
My age: 32
Country: Netherlands
Home town: Oudkarspel
Post code: 1724 Xg
Street: Waterlelie 22

my page - www.hostgator1centcoupon.info

The graphs of the sine and cosine functions are sinusoids of different phases.

The sine wave or sinusoid is a mathematical curve that describes a smooth repetitive oscillation. It is named after the function sine, of which it is the graph. It occurs often in pure and applied mathematics, as well as physics, engineering, signal processing and many other fields. Its most basic form as a function of time (t) is:

$y(t)=A\sin(2\pi ft+\phi )=A\sin(\omega t+\phi )$

where:

• A, the amplitude, is the peak deviation of the function from zero.
• f, the ordinary frequency, is the number of oscillations (cycles) that occur each second of time.
• ω = 2πf, the angular frequency, is the rate of change of the function argument in units of radians per second
• φ, the phase, specifies (in radians) where in its cycle the oscillation is at t = 0.
  • When φ is non-zero, the entire waveform appears to be shifted in time by the amount φ/ω seconds. A negative value represents a delay, and a positive value represents an advance.

My name is Darrel Skirving but everybody calls me Darrel. I'm from Great Britain. I'm studying at the university (2nd year) and I play the Lute for 9 years. Usually I choose music from the famous films :D.
I have two sister. I love Motor sports, watching TV (The Simpsons) and Fencing.

Look at my blog; Hostgator 1 Cent Coupon

The oscillation of an undamped spring-mass system around the equilibrium is a sine wave.

The sine wave is important in physics because it retains its waveshape when added to another sine wave of the same frequency and arbitrary phase and magnitude. It is the only periodic waveform that has this property. This property leads to its importance in Fourier analysis and makes it acoustically unique.

General form

In general, the function may also have:

• a spatial variable x that represents the position on the dimension on which the wave propagates, and a characteristic parameter k called wavenumber (or angular wave number), which represents the proportionality between the angular frequency ω and the linear speed (speed of propagation) ν
• a non-zero center amplitude, D

which is

$y(x,t)=A\sin(kx-\omega t+\phi )+D\,$, if the wave is moving to the right

$y(x,t)=A\sin(kx+\omega t+\phi )+D\,$, if the wave is moving to the left

The wavenumber is related to the angular frequency by:.

$k={\omega \over v}={2\pi f \over v}={2\pi \over \lambda }$

where λ is the wavelength, f is the frequency, and v is the linear speed.

This equation gives a sine wave for a single dimension, thus the generalized equation given above gives the amplitude of the wave at a position x at time t along a single line. This could, for example, be considered the value of a wave along a wire.

In two or three spatial dimensions, the same equation describes a travelling plane wave if position x and wavenumber k are interpreted as vectors, and their product as a dot product. For more complex waves such as the height of a water wave in a pond after a stone has been dropped in, more complex equations are needed.

Occurrences

Illustrating the cosine wave's fundamental relationship to the circle.

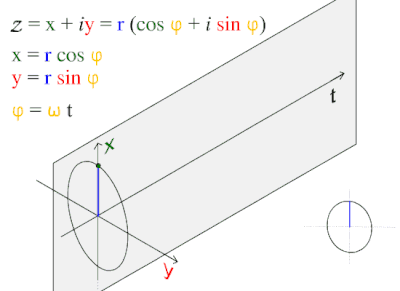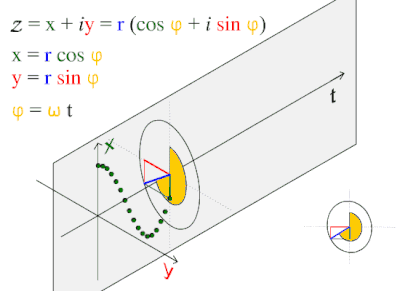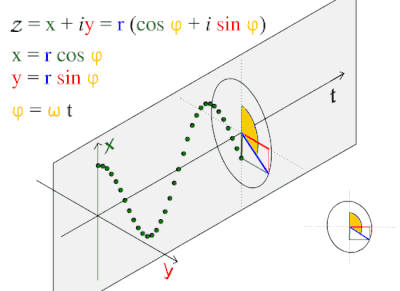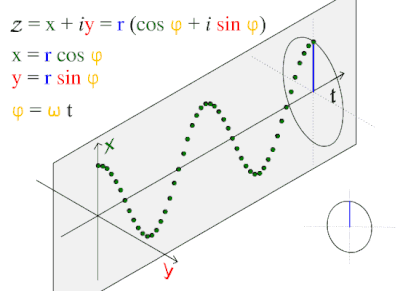
This wave pattern occurs often in nature, including ocean waves, sound waves, and light waves.

A cosine wave is said to be "sinusoidal", because $\cos(x)=\sin(x+\pi /2),$ which is also a sine wave with a phase-shift of π/2. Because of this "head start", it is often said that the cosine function leads the sine function or the sine lags the cosine.

The human ear can recognize single sine waves as sounding clear because sine waves are representations of a single frequency with no harmonics; some sounds that approximate a pure sine wave are whistling, a crystal glass set to vibrate by running a wet finger around its rim, and the sound made by a tuning fork.

To the human ear, a sound that is made of more than one sine wave will have perceptible harmonics; addition of different sine waves results in a different waveform and thus changes the timbre of the sound. Presence of higher harmonics in addition to the fundamental causes variation in the timbre, which is the reason why the same musical note (the same frequency) played on different instruments sounds differently. On the other hand, if the sound contains aperiodic waves along with sine waves (which are periodic), then the sound will be perceived "noisy" as noise is characterized as being aperiodic or having a non-repetitive pattern.

Fourier series

Sine, square, triangle, and sawtooth waveforms

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

In 1822, Joseph Fourier, a French mathematician, discovered that sinusoidal waves can be used as simple building blocks to describe and approximate any periodic waveform including square waves. Fourier used it as an analytical tool in the study of waves and heat flow. It is frequently used in signal processing and the statistical analysis of time series.

Traveling and standing waves

Since sine waves propagate without changing form in distributed linear systems, they are often used to analyze wave propagation. Sine waves traveling in two directions can be represented as

$y(t)=A\sin(kx-\omega t)$ and $y(t)=A\sin(kx+\omega t).$

When two waves having the same amplitude and frequency, and traveling in opposite directions, superpose each other, then a standing wave pattern is created. Note that, on a plucked string, the interfering waves are the waves reflected from the fixed end points of the string.Therefore, standing waves occur only at certain frequencies, which are referred to as resonant frequencies and are composed of a fundamental frequency and its higher harmonics. The resonant frequencies of a string are determined by the length between the fixed ends and the tension of the string.

References

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

See also

• Crest (physics)
• Fourier transform
• Harmonic series (mathematics)
• Harmonic series (music)
• Helmholtz equation
• Instantaneous phase
• Pure tone
• Simple harmonic motion
• Sinusoidal model
• Wave (physics)
• Wave equation

Further reading

• Template:Cite web